google s2 希尔伯特曲线

Posted on Edited on In Views:

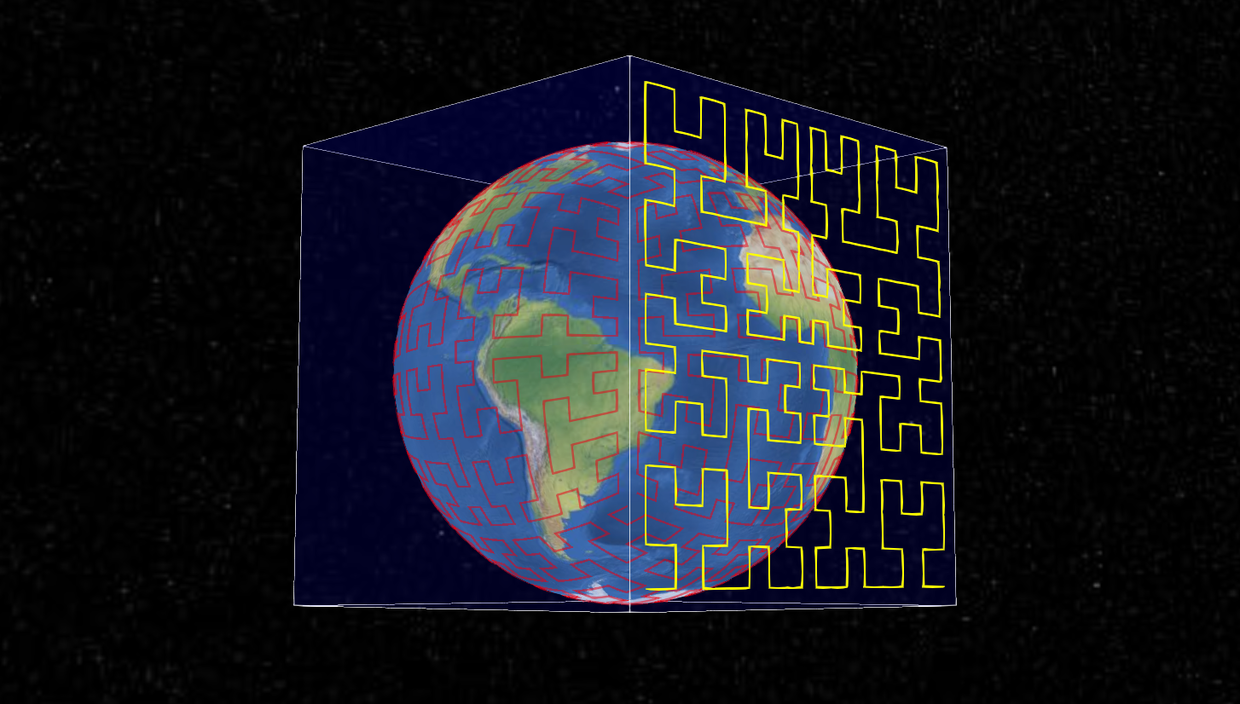
google s2 希尔伯特曲线

S2其实是来自几何数学中N维球面的一个数学符号S²，它表示的是3维空间内的2维球面。S2 这个库其实是被设计用来解决球面上各种几何问题的。

接下来就看看怎么用 S2 来解决多维空间点索引的问题的。

球面坐标转换

众所周知，地球是近似一个球体。球体是一个三维的，如何把三维降成一维呢？

球面上的一个点，在直角坐标系中，可以这样表示：

三维坐标

1
2
3
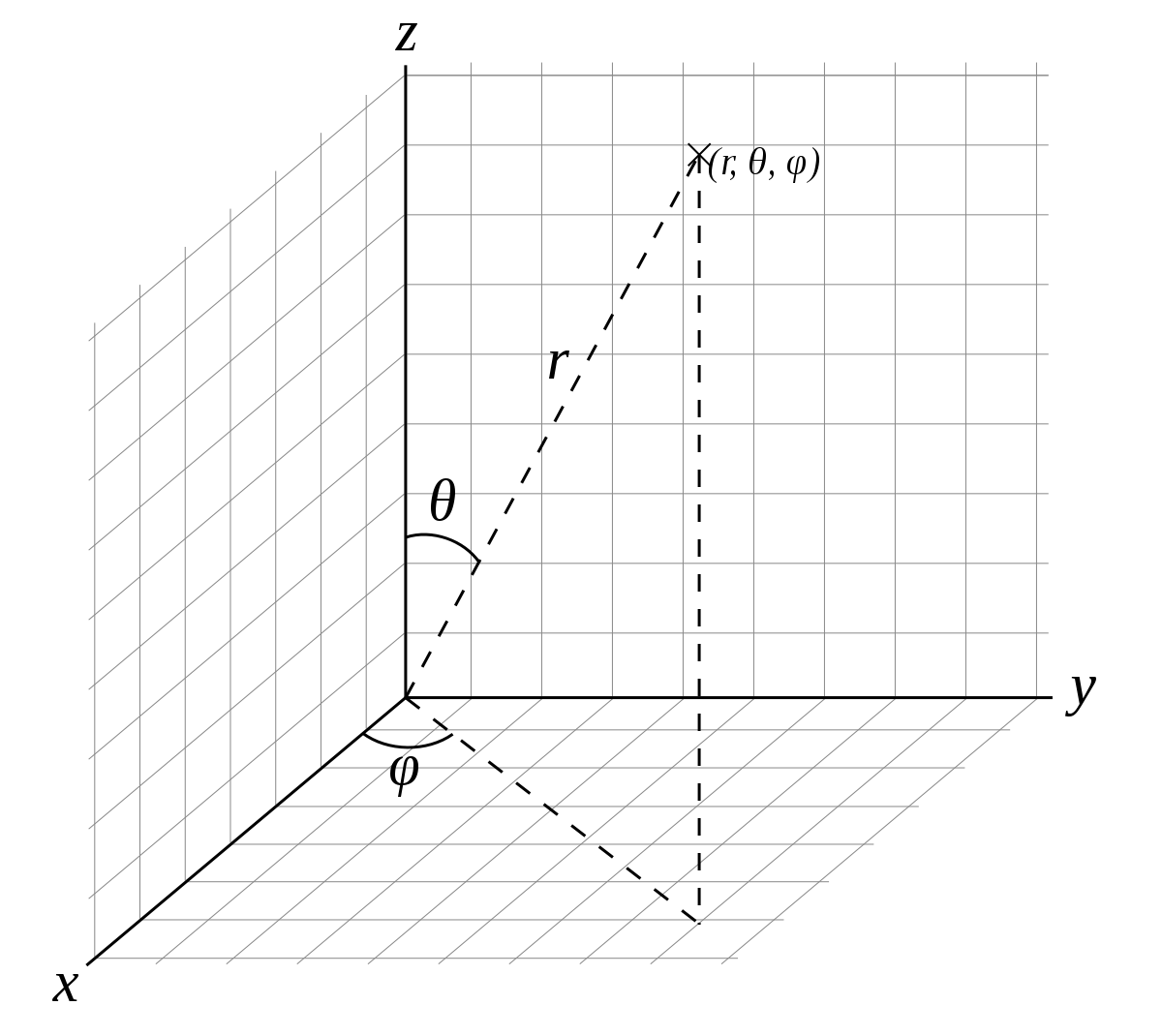
x = r * sin θ * cos φ
y = r * sin θ * sin φ 
z = r * cos θ

通常地球上的点我们会用经纬度来表示。

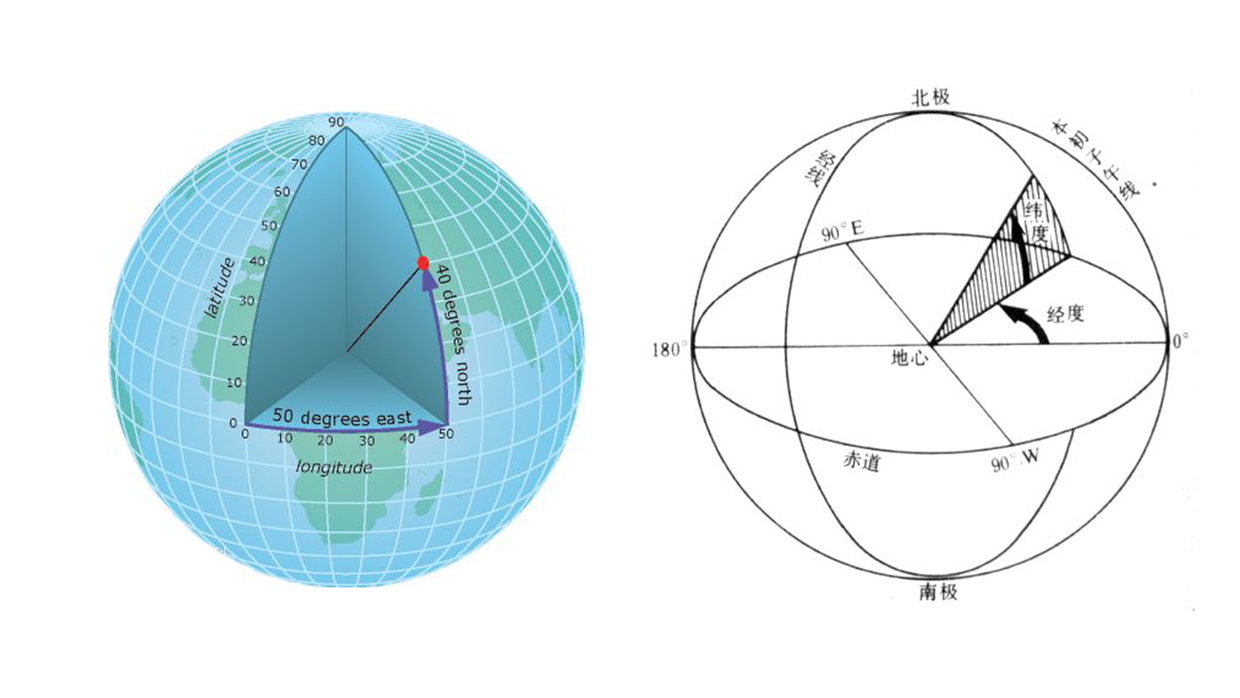
再进一步，我们可以和球面上的经纬度联系起来。不过这里需要注意的是，纬度的角度 α 和直角坐标系下的球面坐标 θ 加起来等于 90°。所以三角函数要注意转换。

于是地球上任意的一个经纬度的点，就可以转换成 f(x,y,z)。

在 S2 中，地球半径被当成单位1了，所以半径不用考虑。x,y,z的值域都被限定在了[-1,1]*[-1,1]*[-1,1]这个区间之内了。

球面变平面

接下来一步 S2 把球面碾成平面。怎么做的呢？

首先在地球外面套了一个外切的正方体，如下图。

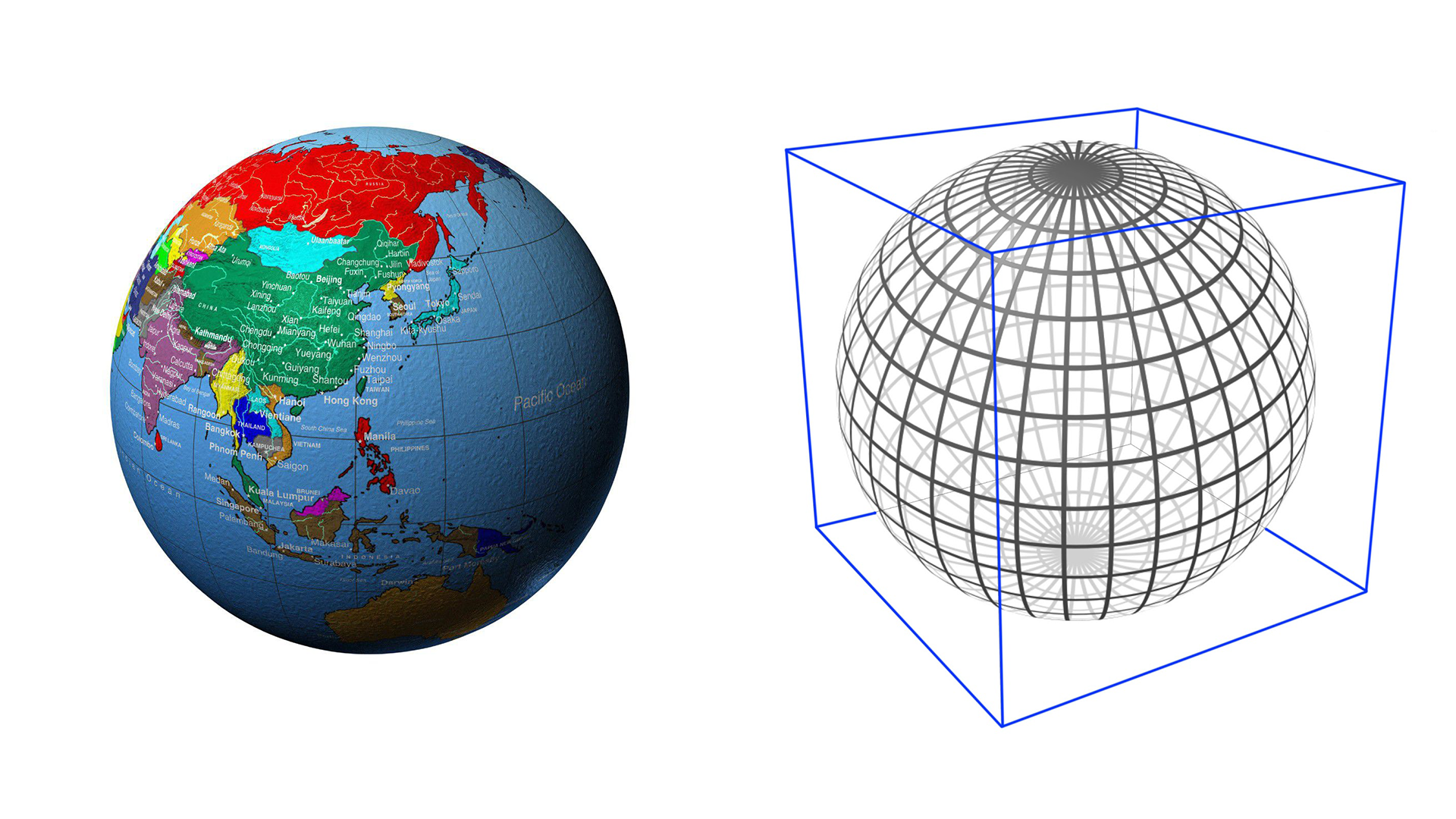
正六边形投影

从球心向外切正方体6个面分别投影。S2 是把球面上所有的点都投影到外切正方体的6个面上。

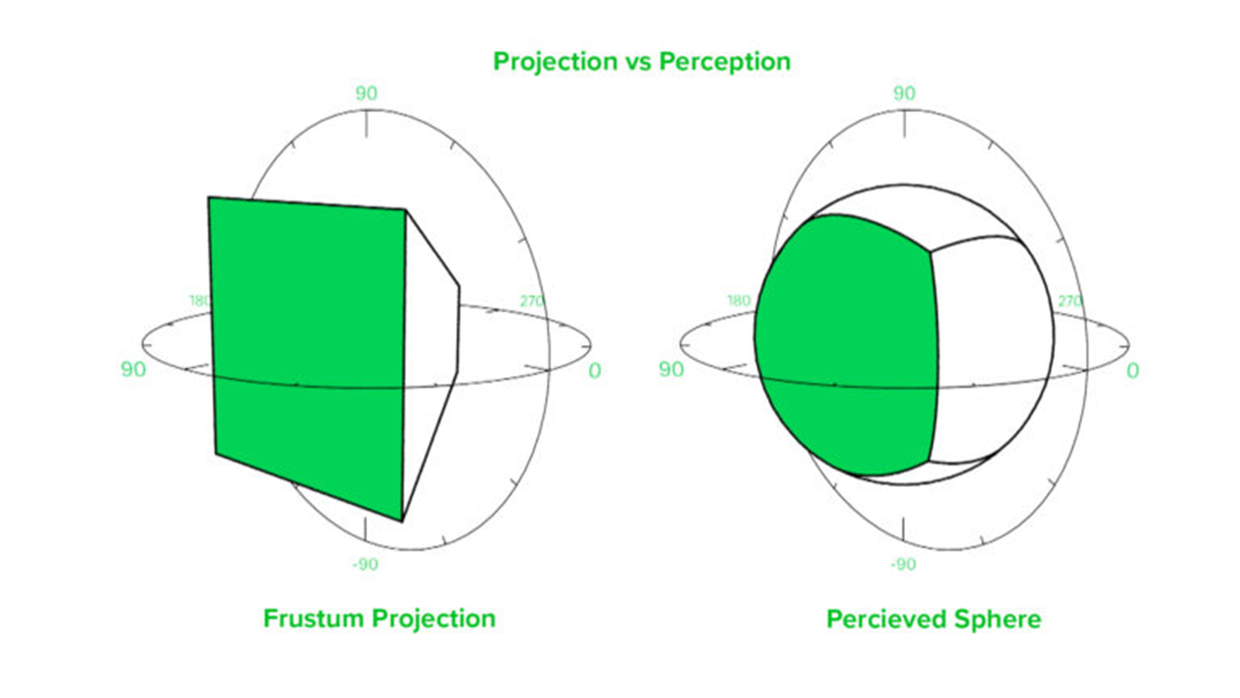
正方体投影

这里简单的画了一个投影图，上图左边的是投影到正方体一个面的示意图，实际上影响到的球面是右边那张图。

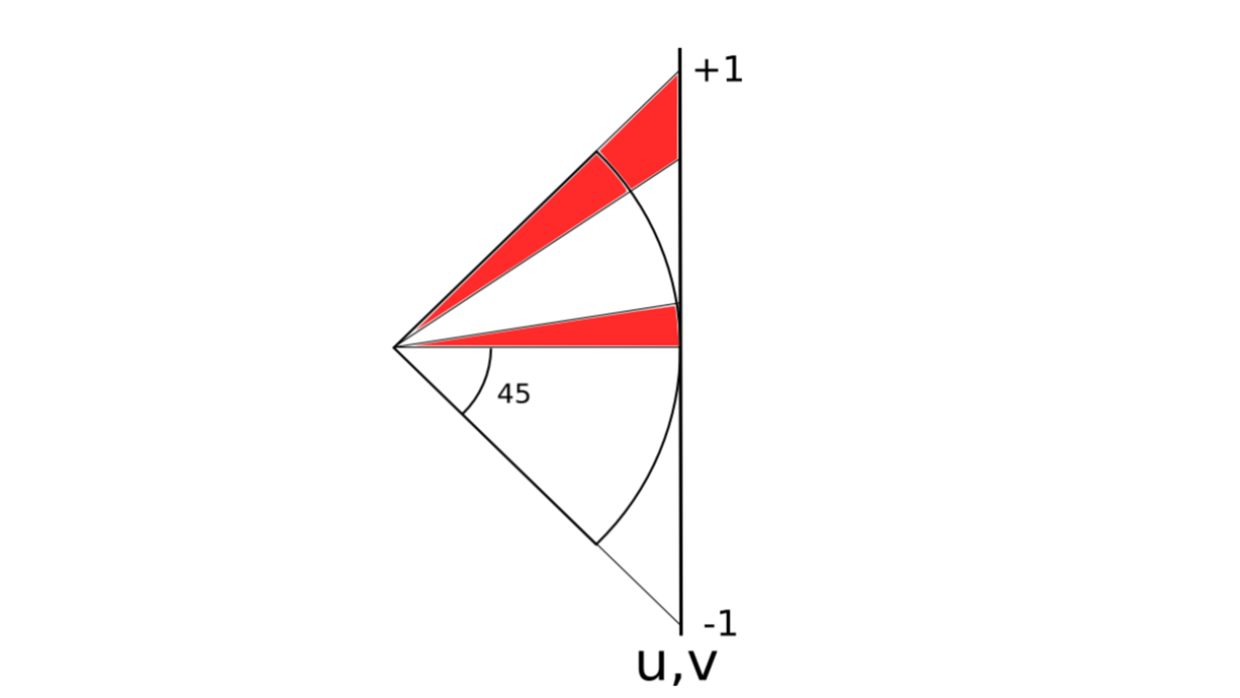
从侧面看，其中一个球面投影到正方体其中一个面上，边缘与圆心的连线相互之间的夹角为90°，但是和x，y，z轴的角度是45°。我们可以在球的6个方向上，把45°的辅助圆画出来，见下图左边。

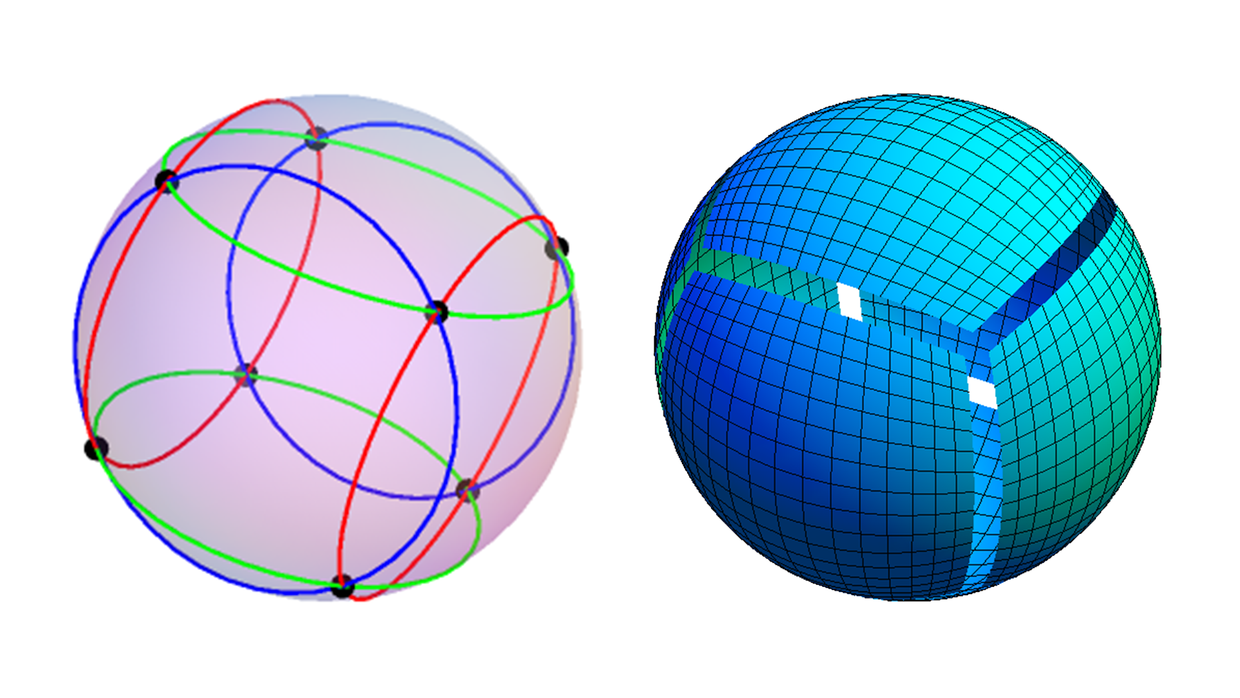
上图左边的图画了6个辅助线，蓝线是前后一对，红线是左右一对，绿线是上下一对。分别都是45°的地方和圆心连线与球面相交的点的轨迹。这样我们就可以把投影到外切正方体6个面上的球面画出来，见上图右边。

投影到正方体以后，我们就可以把这个正方体展开了。

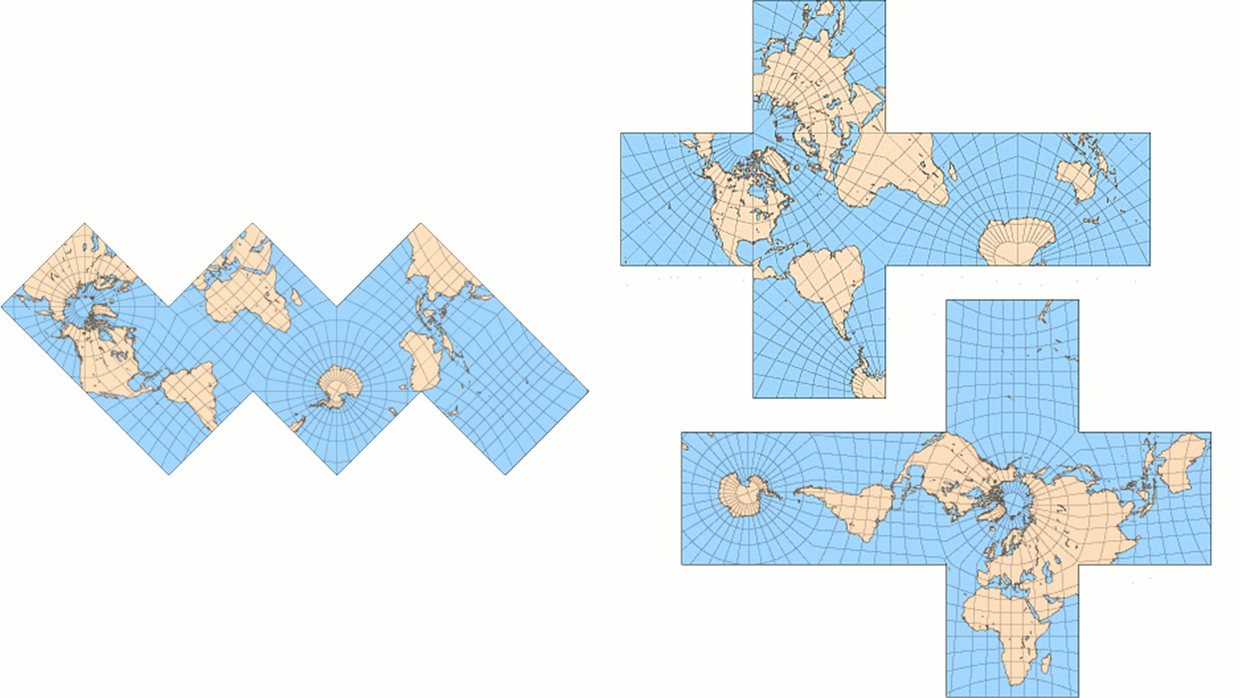
地图正方体投影展开

一个正方体的展开方式有很多种。不管怎么展开，最小单元都是一个正方形。

在 Google S2 中，它是把地球展开成如下的样子：

地球S2投影这样第一步的球面坐标进一步的被转换成 f(x,y,z) -> g(face,u,v)，其中：

face是正方形的6个面(0~5)，u,v对应的是六个面中的一个面上的坐标。

球面矩形投影修正

上一步我们把球面上的球面矩形投影到正方形的某个面上，形成的形状类似于矩形，但是由于球面上角度的不同，最终会导致即使是投影到同一个面上，每个矩形的面积也不大相同。

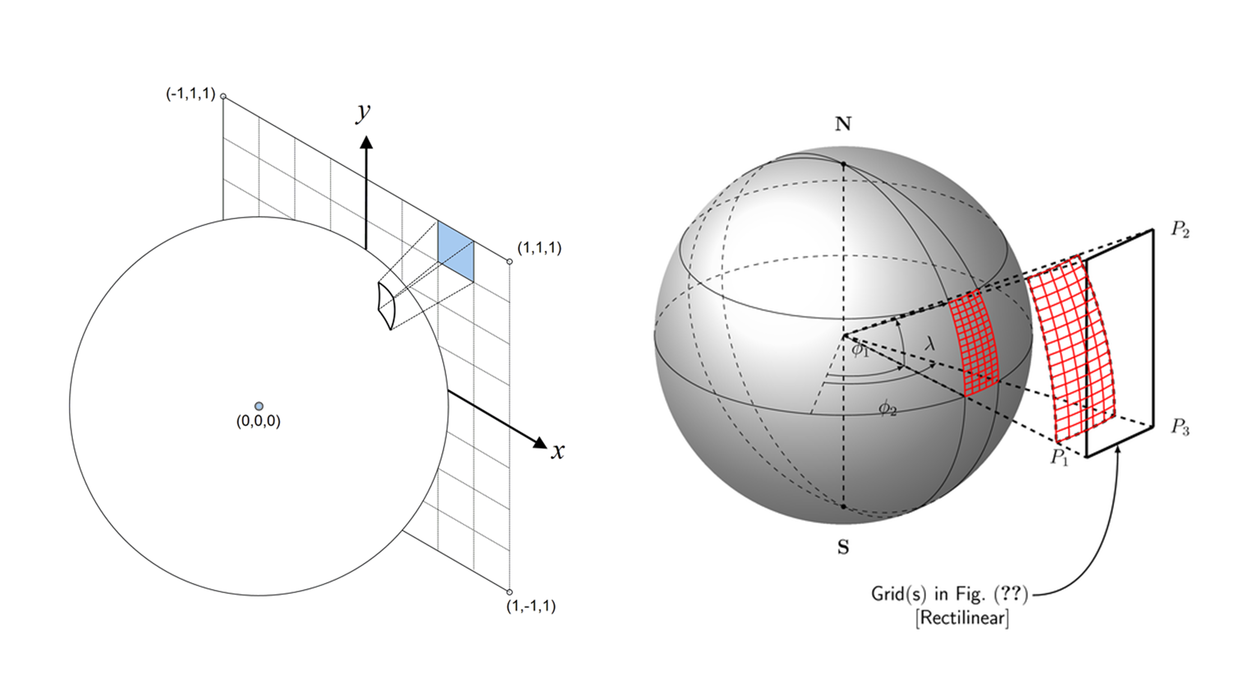
上图就表示出了球面上个一个球面矩形投影到正方形一个面上的情况。

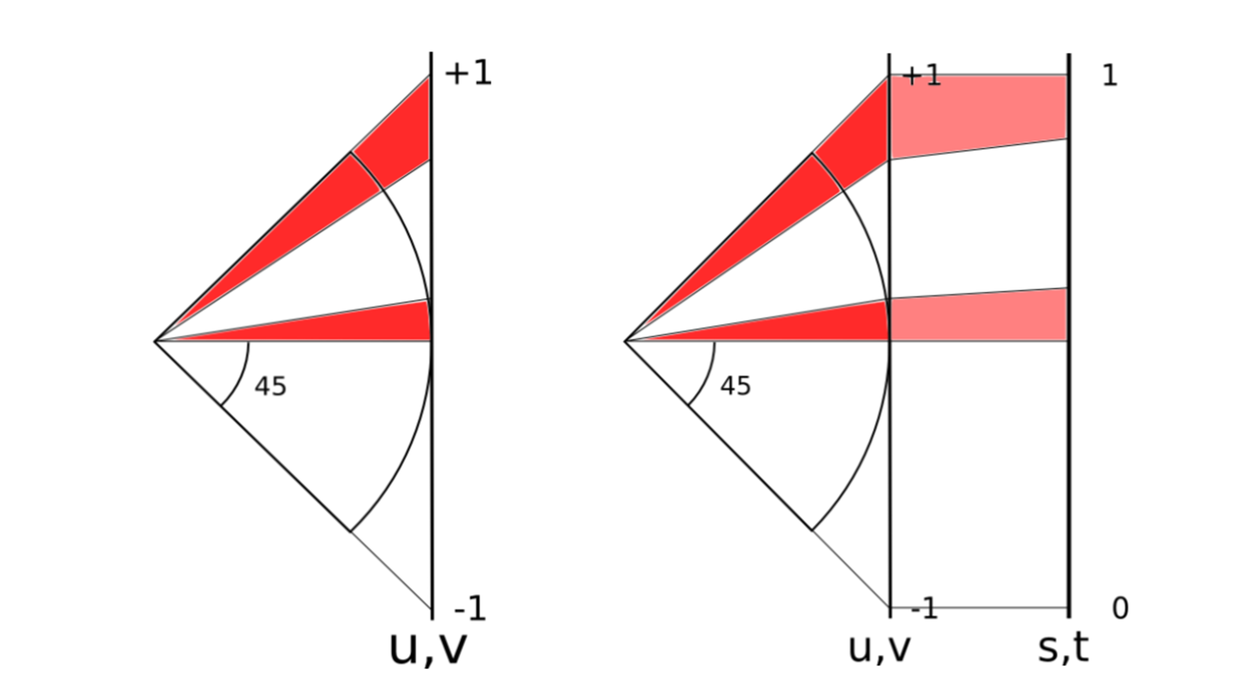
球面投影修正

经过实际计算发现，最大的面积和最小的面积相差5.2倍。见上图左边。相同的弧度区间，在不同的纬度上投影到正方体上的面积不同。

现在就需要修正各个投影出来形状的面积。如何选取合适的映射修正函数就成了关键。目标是能达到上图右边的样子，让各个矩形的面积尽量相同。

这块转换的的不同如下表所示:

面积比率 边比率 对角线比率 ToPointRaw ToPoint FromPoint
线性变换 5.200 2.117 2.959 0.020 0.087 0.085
tan()变换 1.414 1.414 1.704 0.237 0.299 0.258
二次变换 2.082 1.802 1.932 0.033 0.096 0.108

线性变换是最快的变换，但是变换比最小。

tan变换可以使每个投影以后的矩形的面积更加一致，最大和最小的矩形比例仅仅只差0.414。可以说非常接近了。但是 tan函数的调用耗时较长。如果把所有点都按照这种方式计算的话，性能将会降低3倍。

最后google默认选择的是二次变换，这是一个近似切线的投影曲线。它的计算速度远远快于 tan，大概是 tan计算的3倍速度。生成的投影以后的矩形大小也类似。不过最大的矩形和最小的矩形相比依旧有2.082的比率。

上表中，ToPoint和FromPoint 分别是把单位向量转换到 Cell ID 所需要的毫秒数、把 Cell ID 转换回单位向量所需的毫秒数（Cell ID 就是投影到正方体6个面，某个面上矩形的 ID，矩形称为 Cell，它对应的 ID 称为 Cell ID）。ToPointRaw是某种目的下，把 Cell ID 转换为非单位向量所需的毫秒数。

所以投影之后的修正函数三种变换应该如下：

1
2
3
4
5
6
7
8
9
10
// 线性转换
u = 0.5 * ( u + 1)

// tan变换
u = 2 / pi * (atan(u) + pi / 4) = 2 * atan(u) / pi + 0.5

// 二次变换
u >= 0，u = 0.5 * sqrt(1 + 3*u)
u < 0,    u = 1 - 0.5 * sqrt(1 - 3*u)

经过修正变换以后，u，v都变换成了s，t。值域也发生了变化。u，v的值域是[-1,1]，变换以后，是s，t的值域是[0,1]。

至此，小结一下，球面上的点S(lat,lng) -> f(x,y,z) -> g(face,u,v) -> h(face,s,t)。目前总共转换了4步，球面经纬度坐标转换成球面(x,y,z)坐标，再转换成外切正方体投影面上的坐标g(face, u,v)，最后变换成修正后的坐标h(face, s, t)。

点与坐标轴点相互转换

在 S2 算法中，默认划分 Cell 的等级是30，也就是说把一个正方形划分为 2^30 * 2^30个小的正方形。

那么上一步的h(face , s, t)映射到这个正方形上面来，对应该如何转换呢？

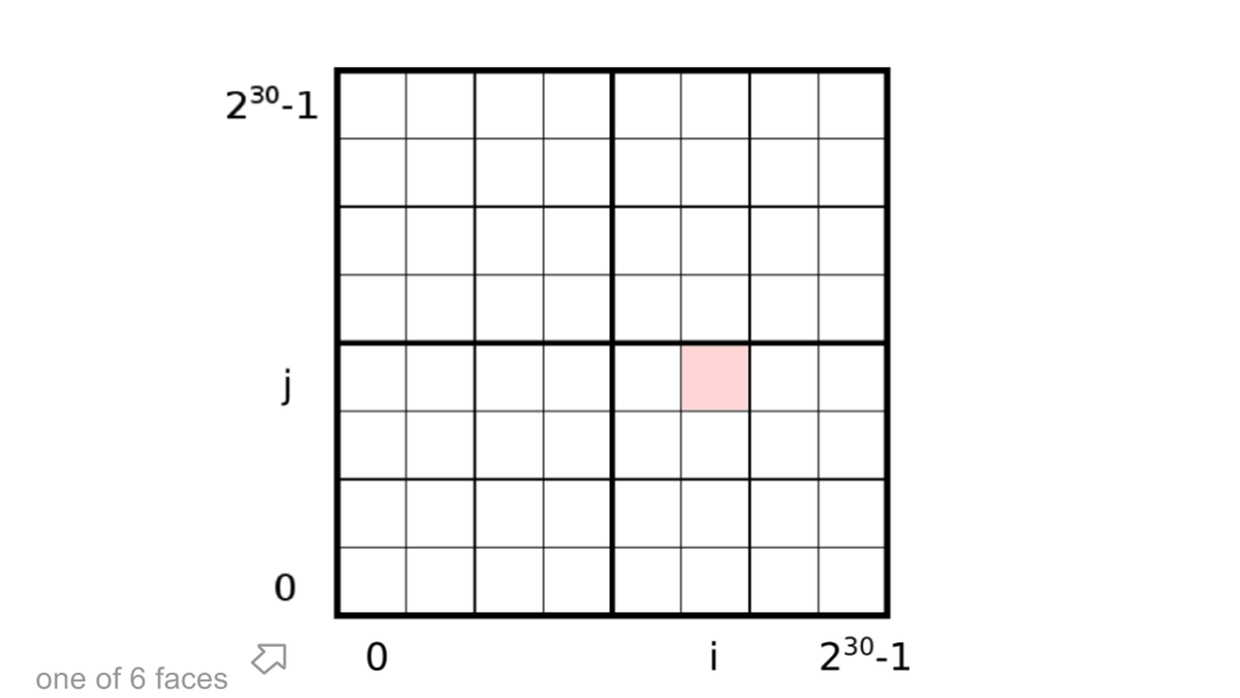
s，t的值域是[0,1]，现在值域要扩大到[0, 2^30-1]。

1
2
3
4
5
6
7
8
inline int S2CellId::STtoIJ(double s) {
  // Converting from floating-point to integers via static_cast is very slow
  // on Intel processors because it requires changing the rounding mode.
  // Rounding to the nearest integer using FastIntRound() is much faster.
  // 这里减去0.5是为了四舍五入
  return max(0, min(kMaxSize - 1, MathUtil::FastIntRound(kMaxSize * s - 0.5)));
}

到这一步，是h(face,s,t) -> H(face,i,j)。

坐标轴点与希尔伯特曲线 Cell ID 相互转换

最后一步，如何把 i，j 和希尔伯特曲线上的点关联起来呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const (
	lookupBits = 4
	swapMask   = 0x01
	invertMask = 0x02
)

var (
	ijToPos = [4][4]int{
		{0, 1, 3, 2}, // canonical order
		{0, 3, 1, 2}, // axes swapped
		{2, 3, 1, 0}, // bits inverted
		{2, 1, 3, 0}, // swapped & inverted
	}
	posToIJ = [4][4]int{
		{0, 1, 3, 2}, // canonical order:    (0,0), (0,1), (1,1), (1,0)
		{0, 2, 3, 1}, // axes swapped:       (0,0), (1,0), (1,1), (0,1)
		{3, 2, 0, 1}, // bits inverted:      (1,1), (1,0), (0,0), (0,1)
		{3, 1, 0, 2}, // swapped & inverted: (1,1), (0,1), (0,0), (1,0)
	}
	posToOrientation = [4]int{swapMask, 0, 0, invertMask | swapMask}
	lookupIJ         [1 << (2*lookupBits + 2)]int
	lookupPos        [1 << (2*lookupBits + 2)]int
)

在变换之前，先来解释一下定义的一些变量。

posToIJ 代表的是一个矩阵，里面记录了一些单元希尔伯特曲线的位置信息。

把 posToIJ 数组里面的信息用图表示出来，如下图：

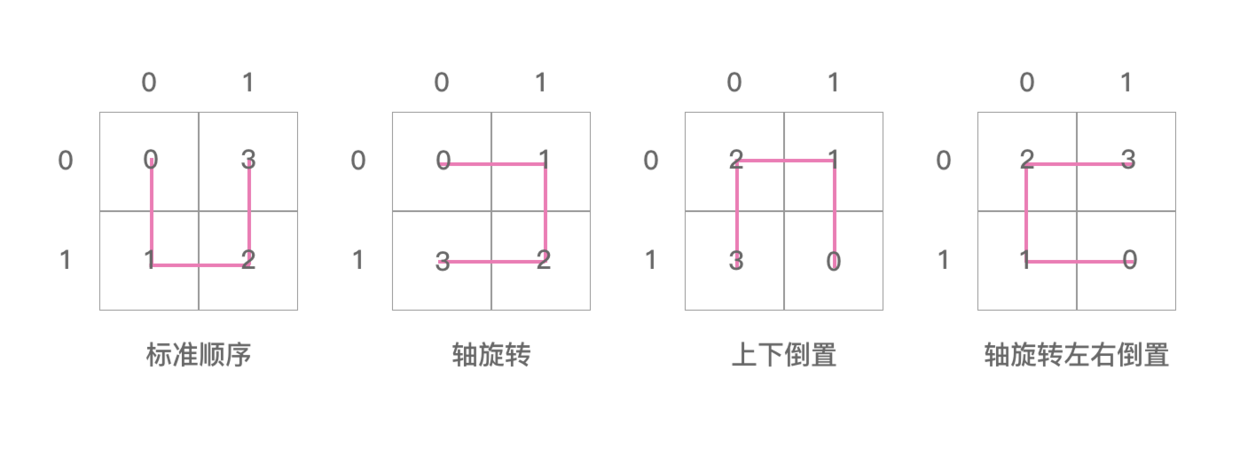
同理，把 ijToPos 数组里面的信息用图表示出来，如下图：

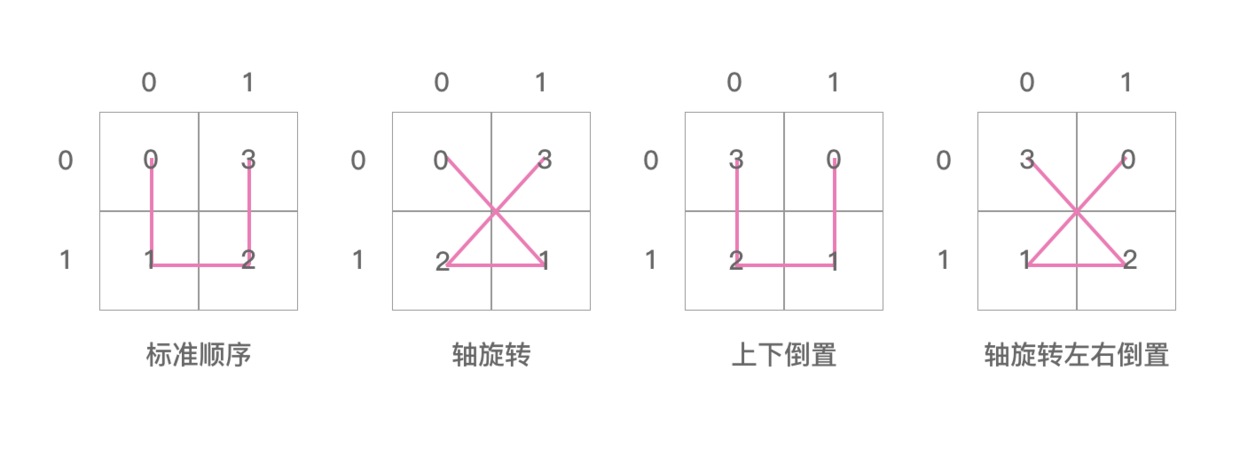
posToOrientation 数组里面装了4个数字，分别是1,0,0,3。
lookupIJ 和 lookupPos 分别是两个容量为1024的数组。这里面分别对应的就是希尔伯特曲线 ID 转换成坐标轴 IJ 的转换表，和坐标轴 IJ 转换成希尔伯特曲线 ID 的转换表。

1
2
3
4
5
6
7
8

func init() {
	initLookupCell(0, 0, 0, 0, 0, 0)
	initLookupCell(0, 0, 0, swapMask, 0, swapMask)
	initLookupCell(0, 0, 0, invertMask, 0, invertMask)
	initLookupCell(0, 0, 0, swapMask|invertMask, 0, swapMask|invertMask)
}

这里是初始化的递归函数，在希尔伯特曲线的标准顺序中可以看到是有4个格子，并且格子都有顺序的，所以初始化要遍历满所有顺序。入参的第4个参数，就是从0 - 3 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// initLookupCell initializes the lookupIJ table at init time.
func initLookupCell(level, i, j, origOrientation, pos, orientation int) {

	if level == lookupBits {
		ij := (i << lookupBits) + j
		lookupPos[(ij<<2)+origOrientation] = (pos << 2) + orientation
		lookupIJ[(pos<<2)+origOrientation] = (ij << 2) + orientation
	
		return
	}

	level++
	i <<= 1
	j <<= 1
	pos <<= 2
	
	r := posToIJ[orientation]
	
	initLookupCell(level, i+(r[0]>>1), j+(r[0]&1), origOrientation, pos, orientation^posToOrientation[0])
	initLookupCell(level, i+(r[1]>>1), j+(r[1]&1), origOrientation, pos+1, orientation^posToOrientation[1])
	initLookupCell(level, i+(r[2]>>1), j+(r[2]&1), origOrientation, pos+2, orientation^posToOrientation[2])
	initLookupCell(level, i+(r[3]>>1), j+(r[3]&1), origOrientation, pos+3, orientation^posToOrientation[3])
}

上面这个函数是生成希尔伯特曲线的。我们可以看到有一处对pos << 2的操作，这里是把位置变换到第一个4个小格子中，所以位置乘以了4。

由于初始设置的lookupBits = 4，所以i，j的变化范围是从[0,15]，总共有16*16=256个，然后i，j坐标是表示的4个格子，再细分，lookupBits = 4这种情况下能表示的点的个数就是256*4=1024个。这也正好是 lookupIJ 和 lookupPos 的总容量。

画一个局部的图，i，j从 0-7 变化。

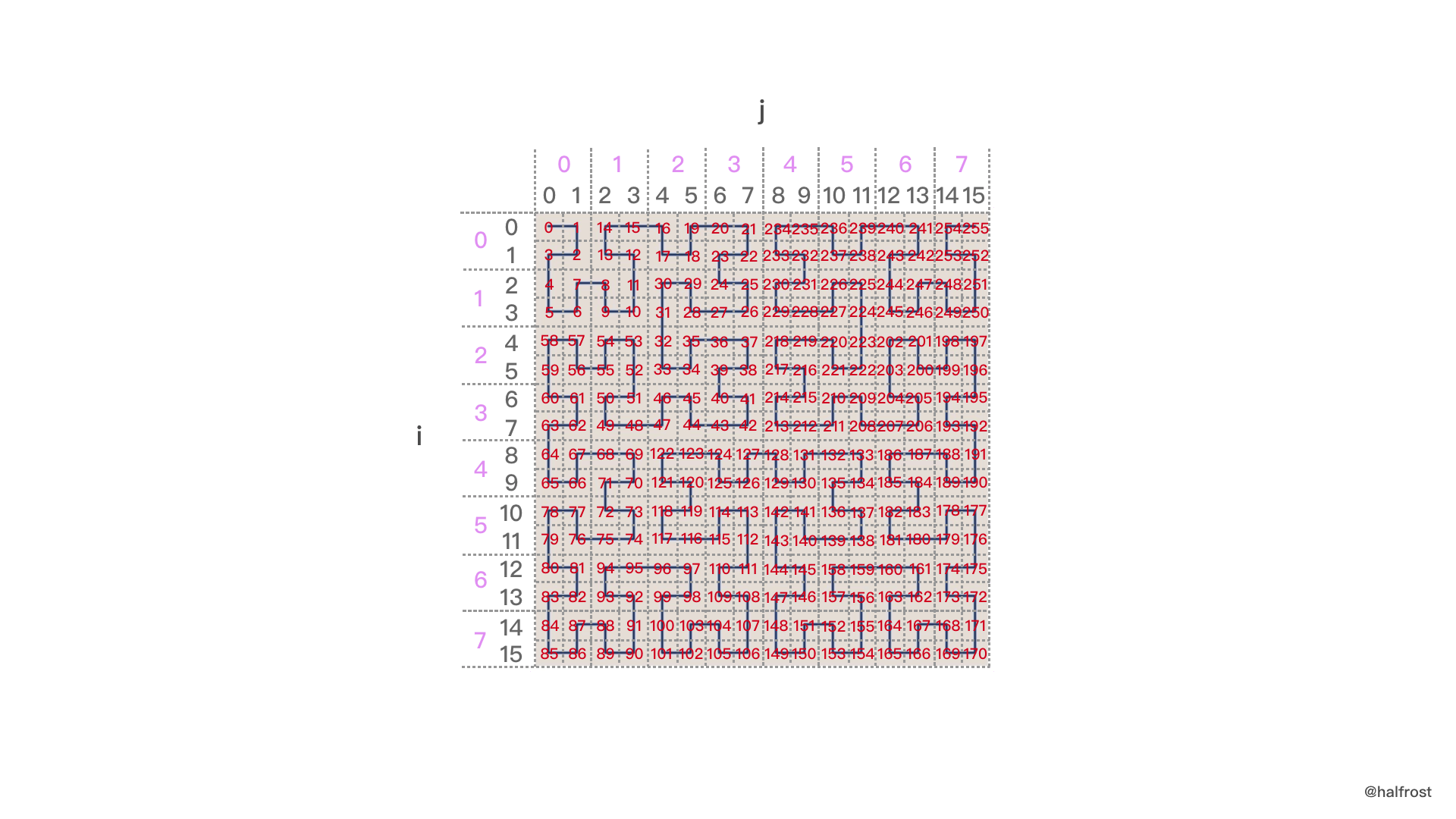
上图是一个4阶希尔伯特曲线。初始化的实际过程就是初始化4阶希尔伯特上的1024个点的坐标与坐标轴上的x，y轴的对应关系表。

举个例子，下表是i，j在递归过程中产生的中间过程。下表是lookupPos 表计算过程。

(i,j) ij ij 计算过程 lookupPos[i j] lookupPos[i j]计算过程 实际坐标
(0,0) 0 0 0 0 (0,0)
(1,0) 64 (1*16+0)*4=64 5 1*4+1=5 (3,0)
(1,1) 68 (1*16+1)*4=68 9 2*4+1=9 (3,2)
(0,1) 4 (0*16+1)*4=4 14 3*4+2=14 (0,2)
(0,2) 8 (0*16+2)*4=8 17 4*4+1=17 (1,4)
(0,3) 12 (0*16+3)*4=12 20 5*4+0=20 (0,6)
(1,3) 76 (1*16+3)*4=76 24 6*4+0=24 (2,6)
(1,2) 72 (1*16+2)*4=72 31 7*4+3=31 (3,4)
(2,2) 136 (2*16+2)*4=136 33 8*4+1=33 (5,4)

取出一行详细分析一下计算过程。

假设当前(i,j)=(0,2)，ij 的计算过程是把 i 左移4位再加上 j，整体结果再左移2位。目的是为了留出2位的方向位置。ij的前4位是i，接着4位是j，最后2位是方向。这样计算出ij的值就是8 。

接着计算lookupPos[i j]的值。从上图中可以看到(0,2)代表的单元格的4个数字是16，17，18，19 。计算到这一步，pos的值为4（pos是专门记录生成格子到第几个了，总共pos的值会循环0-255）。pos代表的是当前是第几个格子(4个小格子组成)，当前是第4个，每个格子里面有4个小格子。所以4*4就可以偏移到当前格子的第一个数字，也就是16 。posToIJ 数组里面会记录下当前格子的形状。从这里我们从中取出 orientation 。

看上图，16，17，18，19对应的是 posToIJ 数组轴旋转的情况，所以17是位于轴旋转图的数字1代表的格子中。这时 orientation = 1 。

这样 lookupPos[i j] 表示的数字就计算出来了，4*4+1=17 。这里就完成了i，j与希尔伯特曲线上数字的对应。

那如何由希尔伯特曲线上的数字对应到实际的坐标呢？

lookupIJ 数组里面记录了反向的信息。lookupIJ 数组 和 lookupPos 数组存储的信息正好是反向的。lookupIJ 数组 下表存的值是 lookupPos 数组 的下表。我们查 lookupIJ 数组 ，lookupIJ[17]的值就是8，对应算出来(i,j)=(0,2)。这个时候的i，j还是大格子。还是需要借助 posToIJ 数组 里面描述的形状信息。当前形状是轴旋转，之前也知道 orientation = 1，由于每个坐标里面有4个小格子，所以一个i，j代表的是2个小格子，所以需要乘以2，再加上形状信息里面的方向，可以计算出实际的坐标 (0 * 2 + 1 , 2 * 2 + 0) = ( 1，4) 。

至此，整个球面坐标的坐标映射就已经完成了。

球面上的点S(lat,lng) -> f(x,y,z) -> g(face,u,v) -> h(face,s,t) -> H(face,i,j) -> CellID。目前总共转换了6步，球面经纬度坐标转换成球面xyz坐标，再转换成外切正方体投影面上的坐标，最后变换成修正后的坐标，再坐标系变换，映射到 [0,2^30^-1]区间，最后一步就是把坐标系上的点都映射到希尔伯特曲线上。

S2 Cell ID 数据结构

最后需要来谈谈 S2 Cell ID 数据结构，这个数据结构直接关系到不同 Level 对应精度的问题。

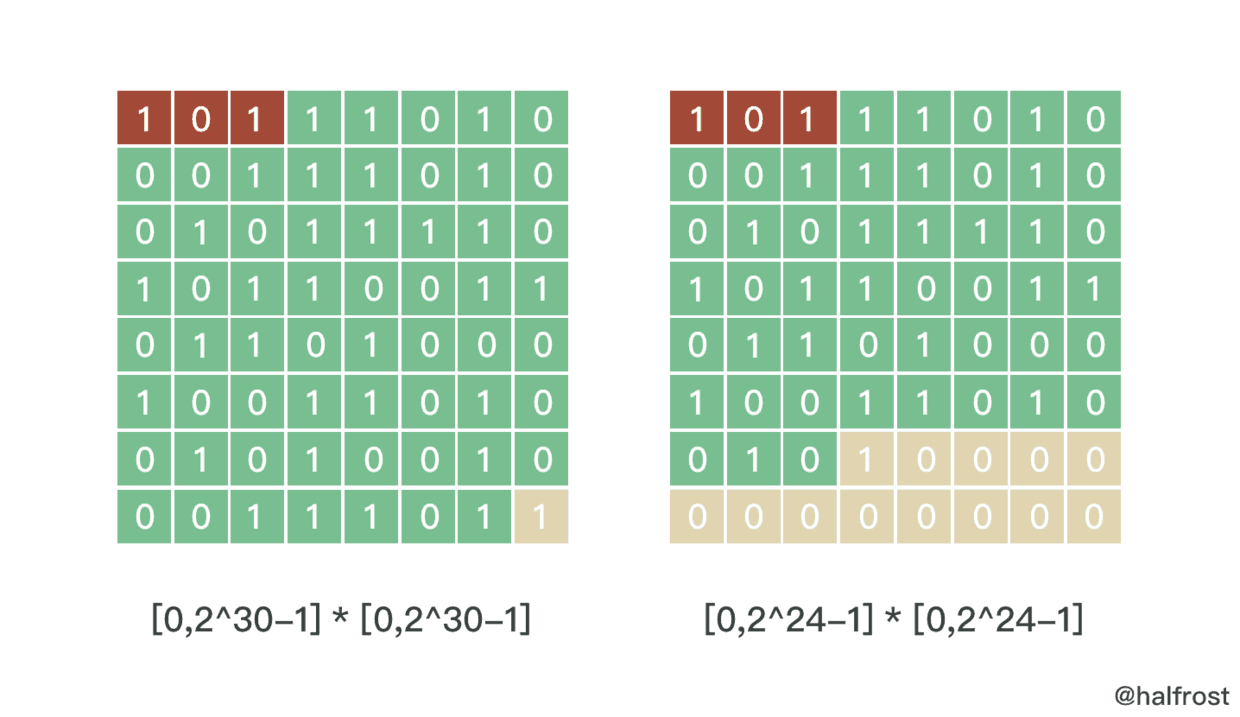
上图左图中对应的是 Level 30 的情况，右图对应的是 Level 24 的情况。(2的多少次方，角标对应的也就是 Level 的值)

在 S2 中，每个 CellID 是由64位的组成的。可以用一个 uint64 存储。开头的3位表示正方体6个面中的一个，取值范围[0,5]。3位可以表示0-7，但是6，7是无效值。

64位的最后一位是1，这一位是特意留出来的。用来快速查找中间有多少位。从末尾最后一位向前查找，找到第一个不为0的位置，即找到第一个1。这一位的前一位到开头的第4位（因为前3位被占用）都是可用数字。

绿色格子有多少个就能表示划分多少格。上图左图，绿色的有60个格子，于是可以表示[0,2^30^ -1] * [0,2^30^ -1]这么多个格子。上图右图中，绿色格子只有48个，那么就只能表示[0,2^24^ -1]*[0,2^24^ -1]这么多个格子。

那么不同 level 可以代表的网格的面积究竟是多大呢？

由上一章我们知道，由于投影的原因，所以导致投影之后的面积依旧有大小差别。

层(level) 最小面积 最大面积 平均面积 单位 Random cell 1 (UK) min edge length Random cell 1 (UK) max edge length Random cell 2 (US) min edge length Random cell 2 (US) max edge length Cell个数
00 85011012.19 85011012.19 85011012.19 km2 7842 km 7842 km 7842 km 7842 km 6
01 21252753.05 21252753.05 21252753.05 km2 3921 km 5004 km 3921 km 5004 km 24
02 4919708.23 6026521.16 5313188.26 km2 1825 km 2489 km 1825 km 2489 km 96
03 1055377.48 1646455.50 1328297.07 km2 840 km 1167 km 1130 km 1310 km 384
04 231564.06 413918.15 332074.27 km2 432 km 609 km 579 km 636 km 1536
05 53798.67 104297.91 83018.57 km2 210 km 298 km 287 km 315 km 6K
06 12948.81 26113.30 20754.64 km2 108 km 151 km 143 km 156 km 24K
07 3175.44 6529.09 5188.66 km2 54 km 76 km 72 km 78 km 98K
08 786.20 1632.45 1297.17 km2 27 km 38 km 36 km 39 km 393K
09 195.59 408.12 324.29 km2 14 km 19 km 18 km 20 km 1573K
10 48.78 102.03 81.07 km2 7 km 9 km 9 km 10 km 6M
11 12.18 25.51 20.27 km2 3 km 5 km 4 km 5 km 25M
12 3.04 6.38 5.07 km2 1699 m 2 km 2 km 2 km 100M
13 0.76 1.59 1.27 km2 850 m 1185 m 1123 m 1225 m 402M
14 0.19 0.40 0.32 km2 425 m 593 m 562 m 613 m 1610M
15 47520.30 99638.93 79172.67 m2 212 m 296 m 281 m 306 m 6B
16 11880.08 24909.73 19793.17 m2 106 m 148 m 140 m 153 m 25B
17 2970.02 6227.43 4948.29 m2 53 m 74 m 70 m 77 m 103B
18 742.50 1556.86 1237.07 m2 27 m 37 m 35 m 38 m 412B
19 185.63 389.21 309.27 m2 13 m 19 m 18 m 19 m 1649B
20 46.41 97.30 77.32 m2 7 m 9 m 9 m 10 m 7T
21 11.60 24.33 19.33 m2 3 m 5 m 4 m 5 m 26T
22 2.90 6.08 4.83 m2 166 cm 2 m 2 m 2 m 105T
23 0.73 1.52 1.21 m2 83 cm 116 cm 110 cm 120 cm 422T
24 0.18 0.38 0.30 m2 41 cm 58 cm 55 cm 60 cm 1689T
25 453.19 950.23 755.05 cm2 21 cm 29 cm 27 cm 30 cm 7e15
26 113.30 237.56 188.76 cm2 10 cm 14 cm 14 cm 15 cm 27e15
27 28.32 59.39 47.19 cm2 5 cm 7 cm 7 cm 7 cm 108e15
28 7.08 14.85 11.80 cm2 2 cm 4 cm 3 cm 4 cm 432e15
29 1.77 3.71 2.95 cm2 12 mm 18 mm 17 mm 18 mm 1729e15
30 0.44 0.93 0.74 cm2 6 mm 9 mm 8 mm 9 mm 7e18

level 0 就是正方体的六个面之一。地球表面积约等于510,100,000 km^2。level 0 的面积就是地球表面积的六分之一。level 30 能表示的最小的面积0.48cm^2，最大也就0.93cm^2 。

S2 与 Geohash 对比

Geohash 有12级，从5000km 到 3.7cm。中间每一级的变化比较大。有时候可能选择上一级会大很多，选择下一级又会小一些。比如选择字符串长度为4，它对应的 cell 宽度是39.1km，需求可能是50km，那么选择字符串长度为5，对应的 cell 宽度就变成了156km，瞬间又大了3倍了。这种情况选择多长的 Geohash 字符串就比较难选。选择不好，每次判断可能就还需要取出周围的8个格子再次进行判断。Geohash 需要 12 bytes 存储。

S2 有30级，从 0.7cm² 到 85,000,000km² 。中间每一级的变化都比较平缓，接近于4次方的曲线。所以选择精度不会出现 Geohash 选择困难的问题。S2 的存储只需要一个 uint64 即可存下。

S2 库里面不仅仅有地理编码，还有其他很多几何计算相关的库。地理编码只是其中的一小部分。本文没有介绍到的 S2 的实现还有很多很多，各种向量计算，面积计算，多边形覆盖，距离问题，球面球体上的问题，它都有实现。

S2 还能解决多边形覆盖的问题。比如给定一个城市，求一个多边形刚刚好覆盖住这个城市。

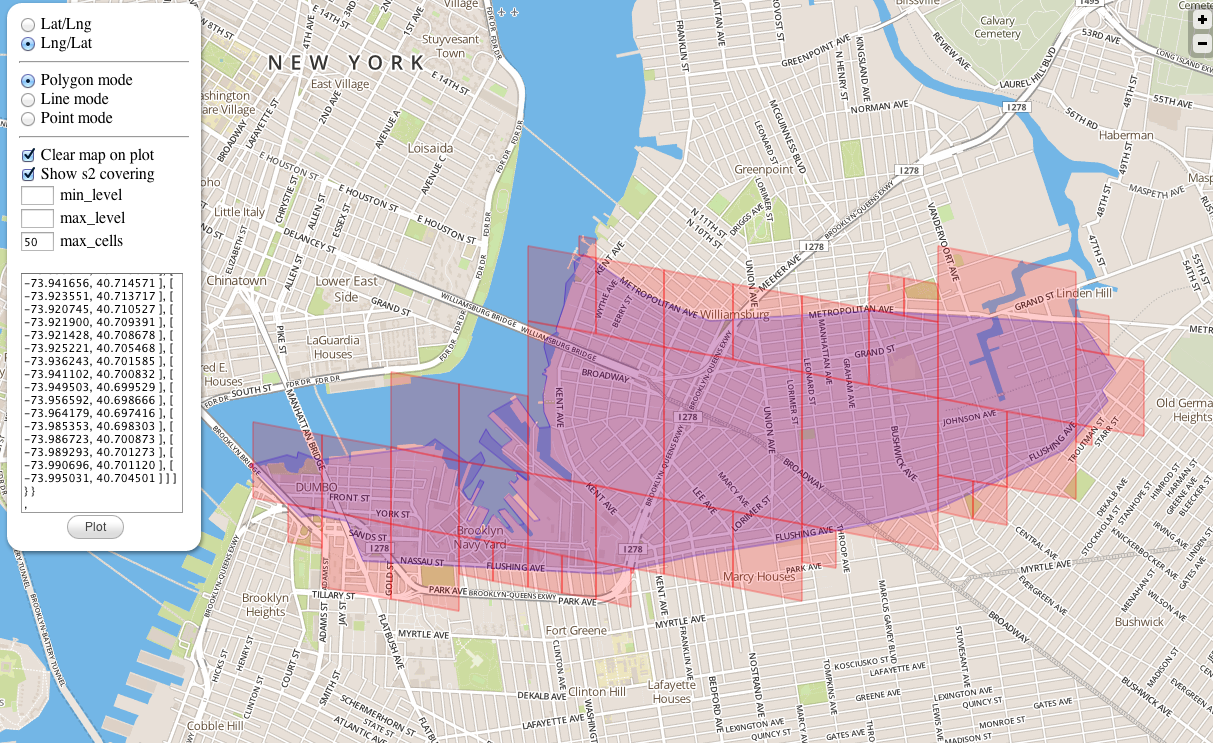
如上图，生成的多边形刚刚好覆盖住下面蓝色的区域。这里生成的多边形可以有大有小。不管怎么样，最终的结果也是刚刚覆盖住目标物。

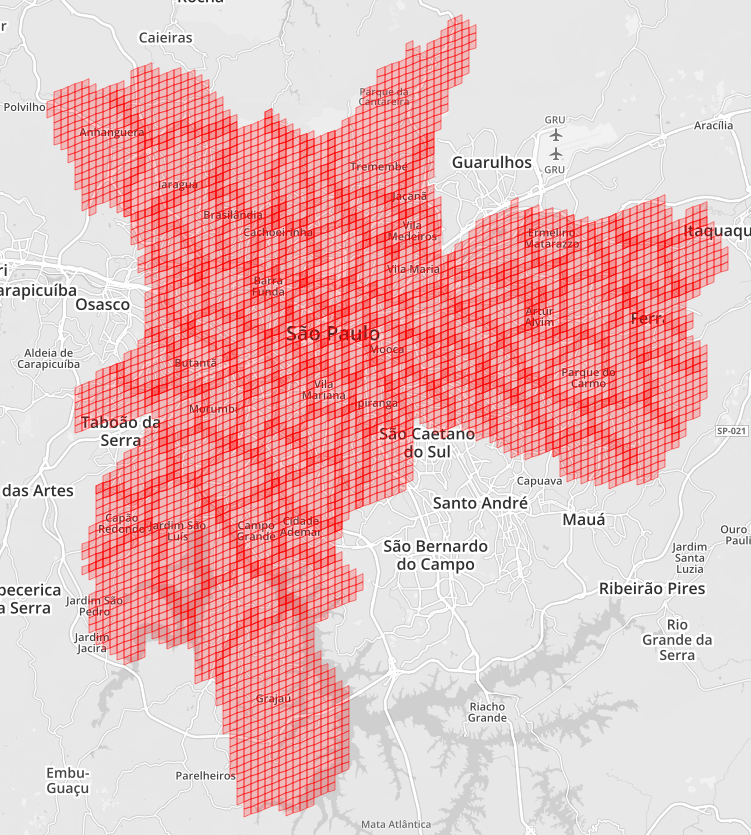
用相同的 Cell 也可以达到相同的目的，上图就是用相同 Level 的 Cell 覆盖了整个圣保罗城市。

这些都是 Geohash 做不到的。

多边形覆盖利用的是近似的算法，虽然不是严格意义上的最优解，但是实践中效果特别好。

额外值得说明的一点是，Google 文档上强调了，这种多边形覆盖的算法虽然对搜索和预处理操作非常有用，但是“不可依赖”的。理由也是因为是近似算法，并不是唯一最优算法，所以得到的解会依据库的不同版本而产生变化。

8. S2 Cell 举例

先来看看经纬度和 CellID 的转换，以及矩形面积的计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
latlng := s2.LatLngFromDegrees(31.232135, 121.41321700000003)
cellID := s2.CellIDFromLatLng(latlng)
cell := s2.CellFromCellID(cellID) //9279882742634381312

// cell.Level()
fmt.Println("latlng = ", latlng)
fmt.Println("cell level = ", cellID.Level())
fmt.Printf("cell = %d\n", cellID)
smallCell := s2.CellFromCellID(cellID.Parent(10))
fmt.Printf("smallCell level = %d\n", smallCell.Level())
fmt.Printf("smallCell id = %b\n", smallCell.ID())
fmt.Printf("smallCell ApproxArea = %v\n", smallCell.ApproxArea())
fmt.Printf("smallCell AverageArea = %v\n", smallCell.AverageArea())
fmt.Printf("smallCell ExactArea = %v\n", smallCell.ExactArea())

这里 Parent 方法参数可以直接指定返回改点的对应 level 的 CellID。

上面那些方法打印出来的结果如下：

1
2
3
4
5
6
7
8
9
10
latlng =  [31.2321350, 121.4132170]
cell level =  30
cell = 3869277663051577529

****Parent **** 10000000000000000000000000000000000000000
smallCell level = 10
smallCell id = 11010110110010011011110000000000000000000000000000000000000000
smallCell ApproxArea = 1.9611002454714756e-06
smallCell AverageArea = 1.997370817559429e-06
smallCell ExactArea = 1.9611009480261058e-06

再举一个覆盖多边形的例子。我们先随便创建一个区域。

1
2
3
4
5
6
rect = s2.RectFromLatLng(s2.LatLngFromDegrees(48.99, 1.852))
rect = rect.AddPoint(s2.LatLngFromDegrees(48.68, 2.75))

rc := &s2.RegionCoverer{MaxLevel: 20, MaxCells: 10, MinLevel: 2}
r := s2.Region(rect.CapBound())
covering := rc.Covering(r)

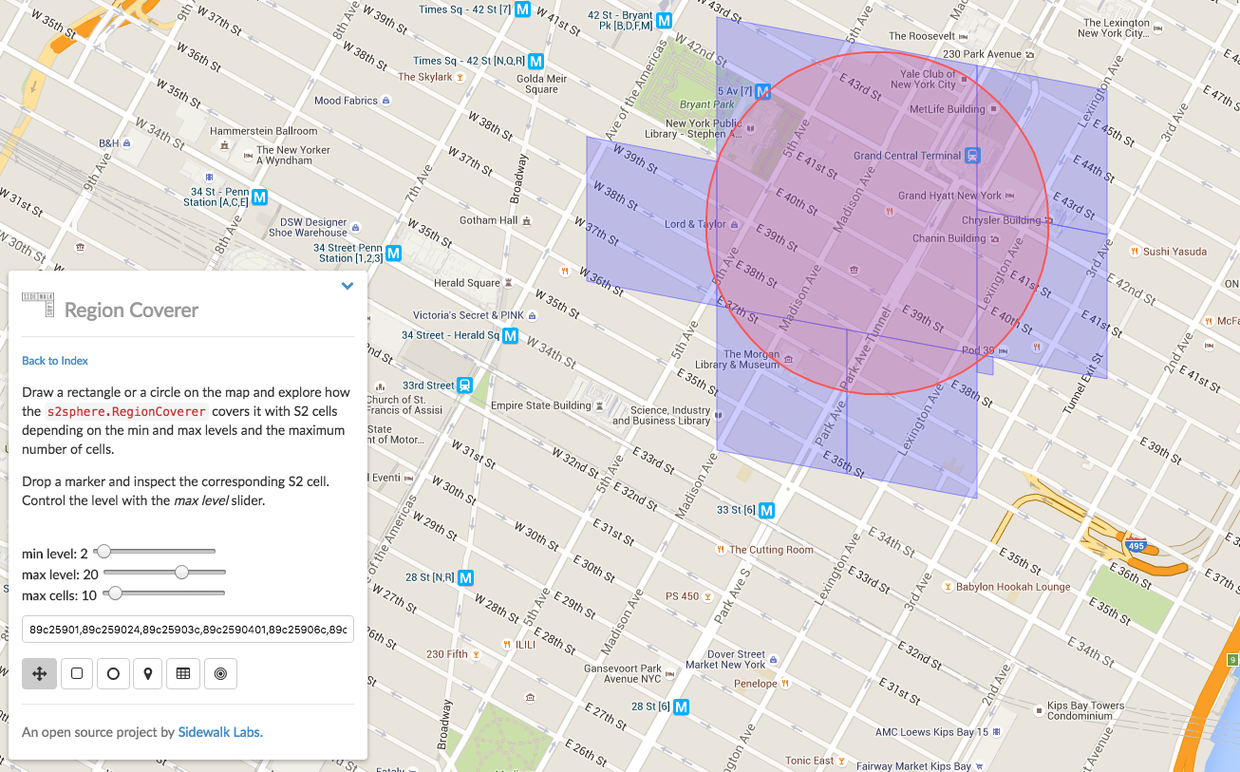
覆盖参数设置成 level 2 - 20，最多的 Cell 的个数是10个。

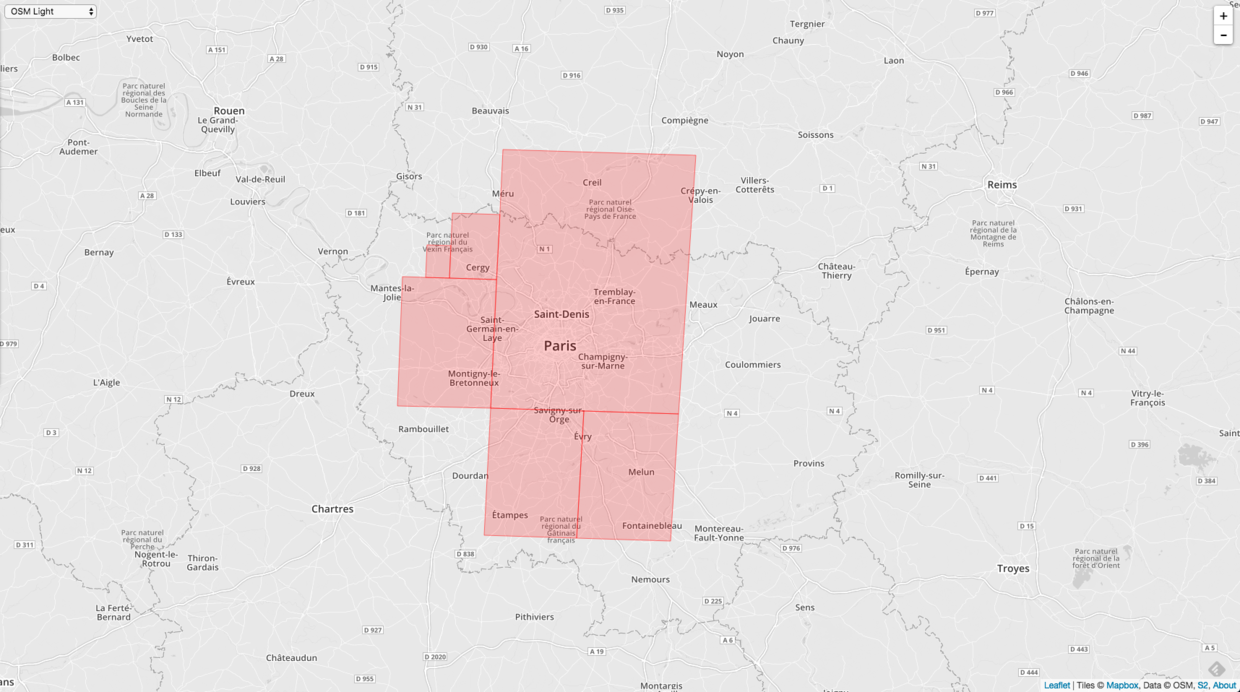
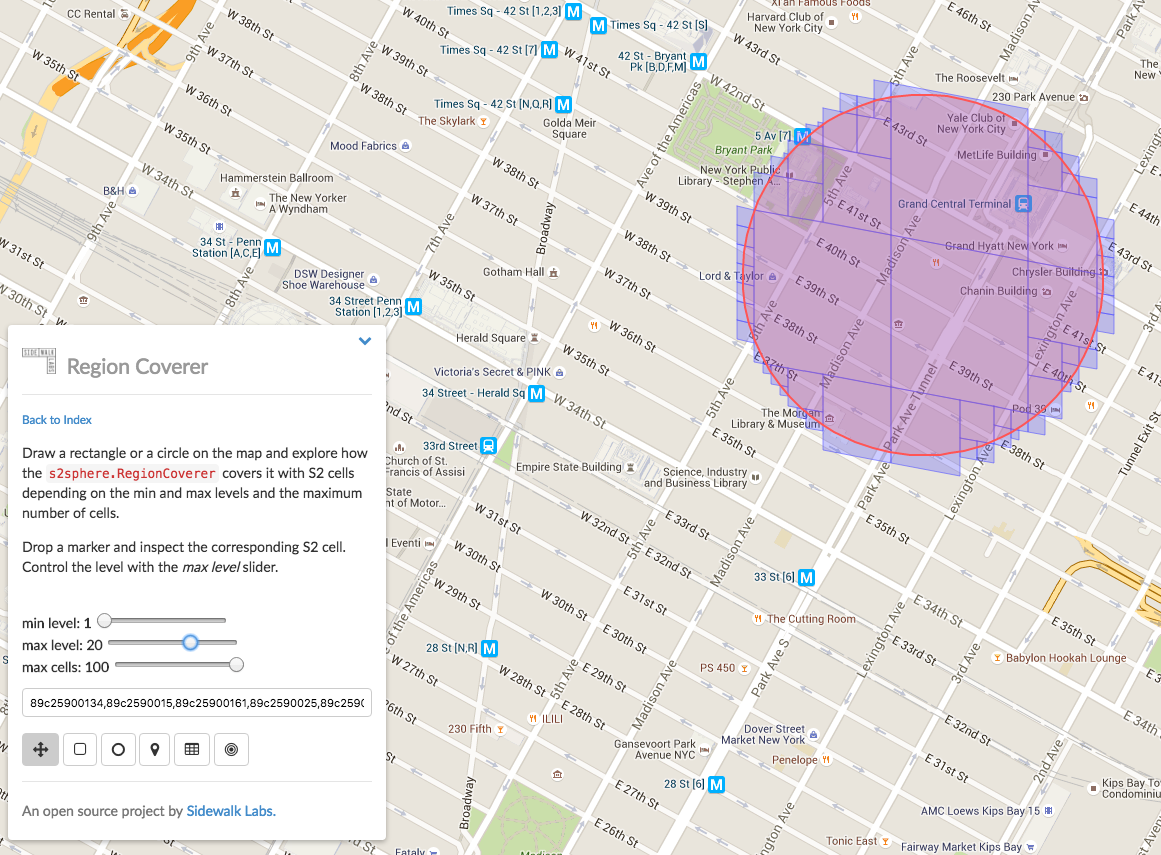
接着我们把 Cell 至多改成20个。

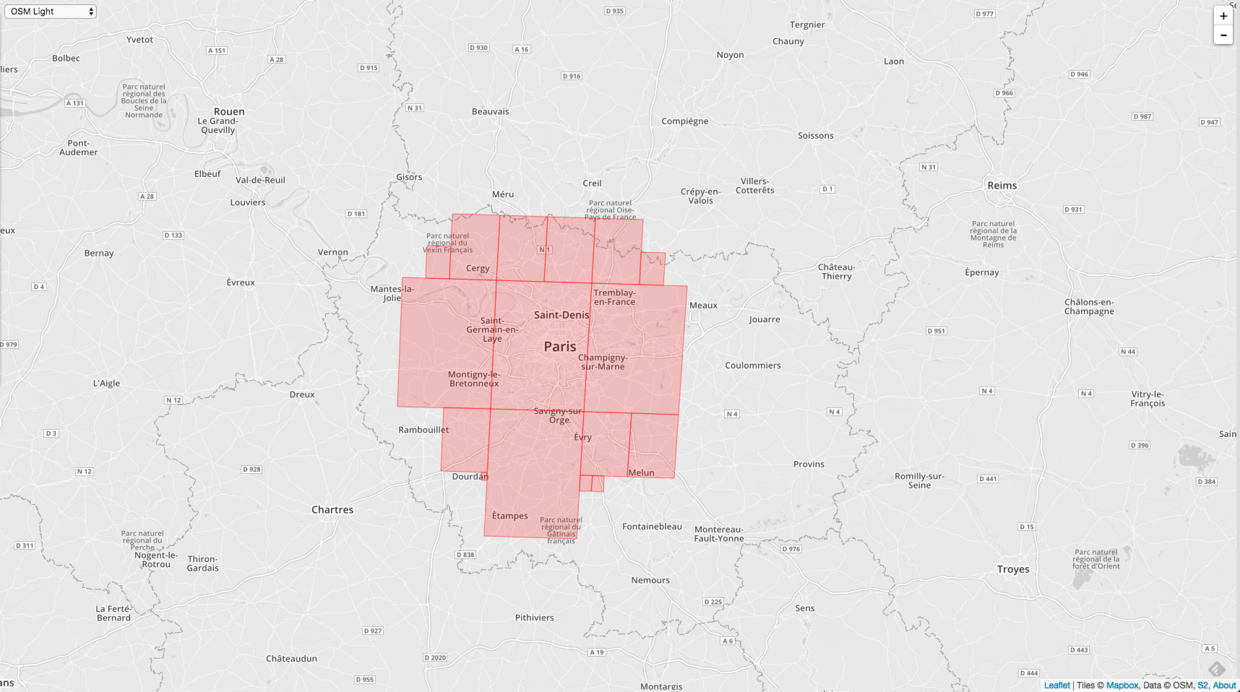
最后再改成30个。

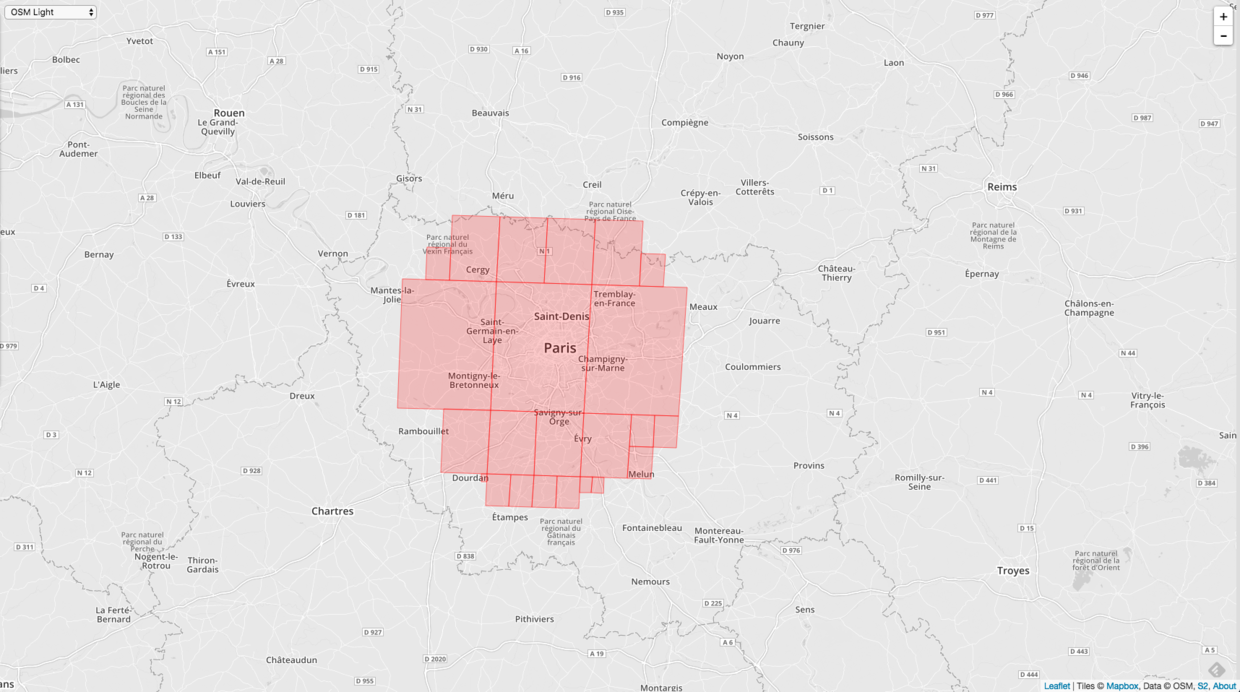
可以看到相同的 level 的范围，cell 个数越多越精确目标范围。

这里是匹配矩形区域，匹配圆形区域也同理。

代码就不贴了，与矩形类似。这种功能 Geohash 就做不到，需要自己手动实现了。

最后举一个多边形匹配的例子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

func testLoop() {
	ll1 := s2.LatLngFromDegrees(31.803269, 113.421145)
	ll2 := s2.LatLngFromDegrees(31.461846, 113.695803)
	ll3 := s2.LatLngFromDegrees(31.250756, 113.756228)
	ll4 := s2.LatLngFromDegrees(30.902604, 113.997927)
	ll5 := s2.LatLngFromDegrees(30.817726, 114.464846)
	ll6 := s2.LatLngFromDegrees(30.850743, 114.76697)
	ll7 := s2.LatLngFromDegrees(30.713884, 114.997683)
	ll8 := s2.LatLngFromDegrees(30.430111, 115.42615)
	ll9 := s2.LatLngFromDegrees(30.088491, 115.640384)
	ll10 := s2.LatLngFromDegrees(29.907713, 115.656863)
	ll11 := s2.LatLngFromDegrees(29.783833, 115.135012)
	ll12 := s2.LatLngFromDegrees(29.712295, 114.728518)
	ll13 := s2.LatLngFromDegrees(29.55473, 114.24512)
	ll14 := s2.LatLngFromDegrees(29.530835, 113.717776)
	ll15 := s2.LatLngFromDegrees(29.55473, 113.3772)
	ll16 := s2.LatLngFromDegrees(29.678892, 112.998172)
	ll17 := s2.LatLngFromDegrees(29.941039, 112.349978)
	ll18 := s2.LatLngFromDegrees(30.040949, 112.025882)
	ll19 := s2.LatLngFromDegrees(31.803269, 113.421145)

	point1 := s2.PointFromLatLng(ll1)
	point2 := s2.PointFromLatLng(ll2)
	point3 := s2.PointFromLatLng(ll3)
	point4 := s2.PointFromLatLng(ll4)
	point5 := s2.PointFromLatLng(ll5)
	point6 := s2.PointFromLatLng(ll6)
	point7 := s2.PointFromLatLng(ll7)
	point8 := s2.PointFromLatLng(ll8)
	point9 := s2.PointFromLatLng(ll9)
	point10 := s2.PointFromLatLng(ll10)
	point11 := s2.PointFromLatLng(ll11)
	point12 := s2.PointFromLatLng(ll12)
	point13 := s2.PointFromLatLng(ll13)
	point14 := s2.PointFromLatLng(ll14)
	point15 := s2.PointFromLatLng(ll15)
	point16 := s2.PointFromLatLng(ll16)
	point17 := s2.PointFromLatLng(ll17)
	point18 := s2.PointFromLatLng(ll18)
	point19 := s2.PointFromLatLng(ll19)

	points := []s2.Point{}
	points = append(points, point19)
	points = append(points, point18)
	points = append(points, point17)
	points = append(points, point16)
	points = append(points, point15)
	points = append(points, point14)
	points = append(points, point13)
	points = append(points, point12)
	points = append(points, point11)
	points = append(points, point10)
	points = append(points, point9)
	points = append(points, point8)
	points = append(points, point7)
	points = append(points, point6)
	points = append(points, point5)
	points = append(points, point4)
	points = append(points, point3)
	points = append(points, point2)
	points = append(points, point1)

	loop := s2.LoopFromPoints(points)

	fmt.Println("----  loop search (gets too much) -----")
	// fmt.Printf("Some loop status items: empty:%t   full:%t \n", loop.IsEmpty(), loop.IsFull())

	// ref: https://github.com/golang/geo/issues/14#issuecomment-257064823
	defaultCoverer := &s2.RegionCoverer{MaxLevel: 20, MaxCells: 1000, MinLevel: 1}
	// rg := s2.Region(loop.CapBound())
	// cvr := defaultCoverer.Covering(rg)
	cvr := defaultCoverer.Covering(loop)

	// fmt.Println(poly.CapBound())
	for _, c3 := range cvr {
		fmt.Printf("%d,\n", c3)
	}
}



这里用到了 Loop 类，这个类的初始化的最小单元是 Point，Point 是由经纬度产生的。最重要的一点需要注意的是，多边形是按照逆时针方向，左手边区域确定的。

如果一不小心点是按照顺时针排列的话，那么多边形确定的是外层更大的面，意味着球面除去画的这个多边形以外的都是你想要的多边形。

举个具体的例子，假如我们想要画的多边形是下图这个样子的：

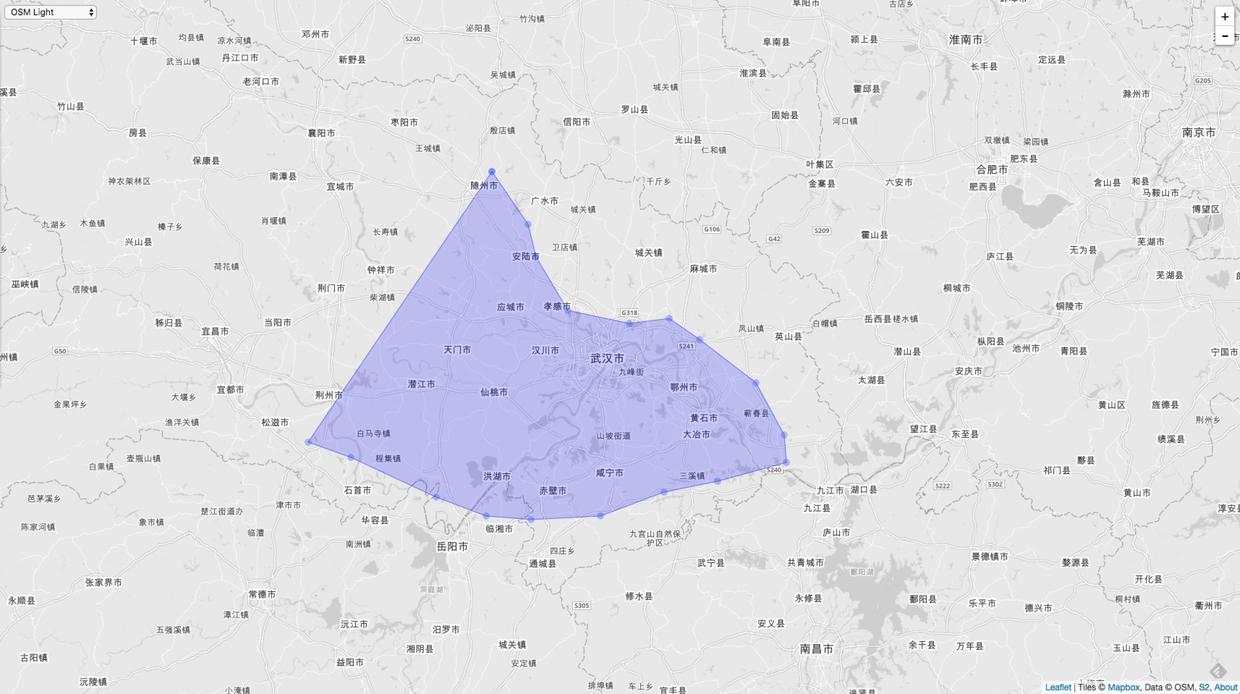
如果我们用顺时针的方式依次存储 Point 的话，并用顺时针的这个数组去初始化 Loop，那么就会出现“奇怪”的现象。如下图：

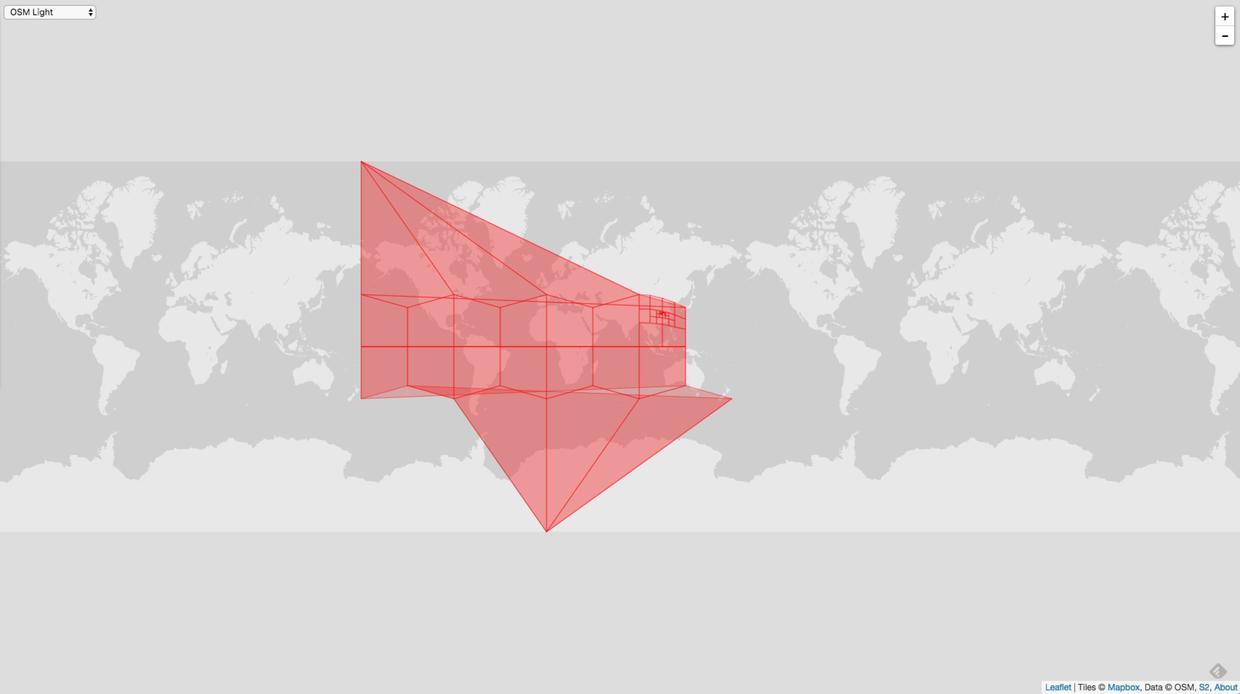
这张图左上角的顶点和右下角的顶点在地球上是重合的。如果把这个地图重新还原成球面，那么就是整个球面中间挖空了一个多边形。

把上图放大，如下图：

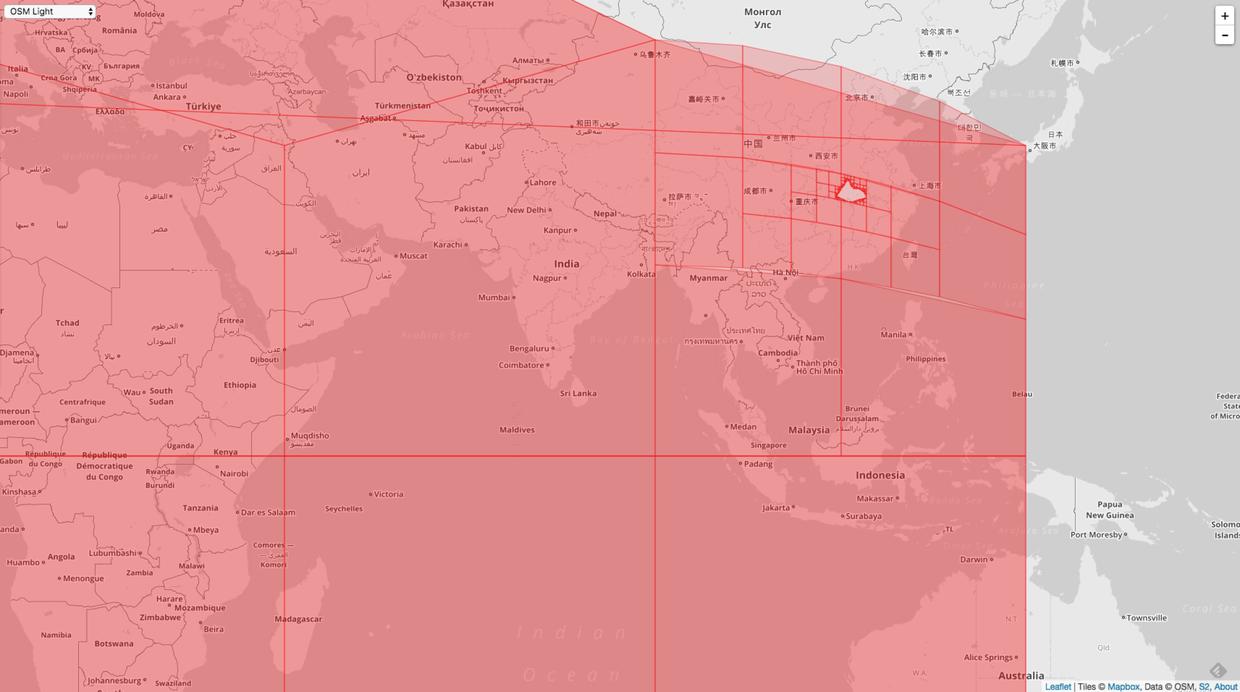
这样就可以很清晰的看到了，中间被挖空了一个多边形。造成这种现象的原因就是按照顺时针的方向存储了每个点，那么初始化一个 Loop 的时候就会选择多边形外圈的更大的多边形。

使用 Loop 一定要切记，顺时针表示的是外圈多边形，逆时针表示的是内圈多边形。

多边形覆盖的问题同之前举的例子一样：

相同的 MaxLevel = 20，MinLevel = 1，MaxCells 不同，覆盖的精度就不同，下图是 MaxCells = 100 的情况：

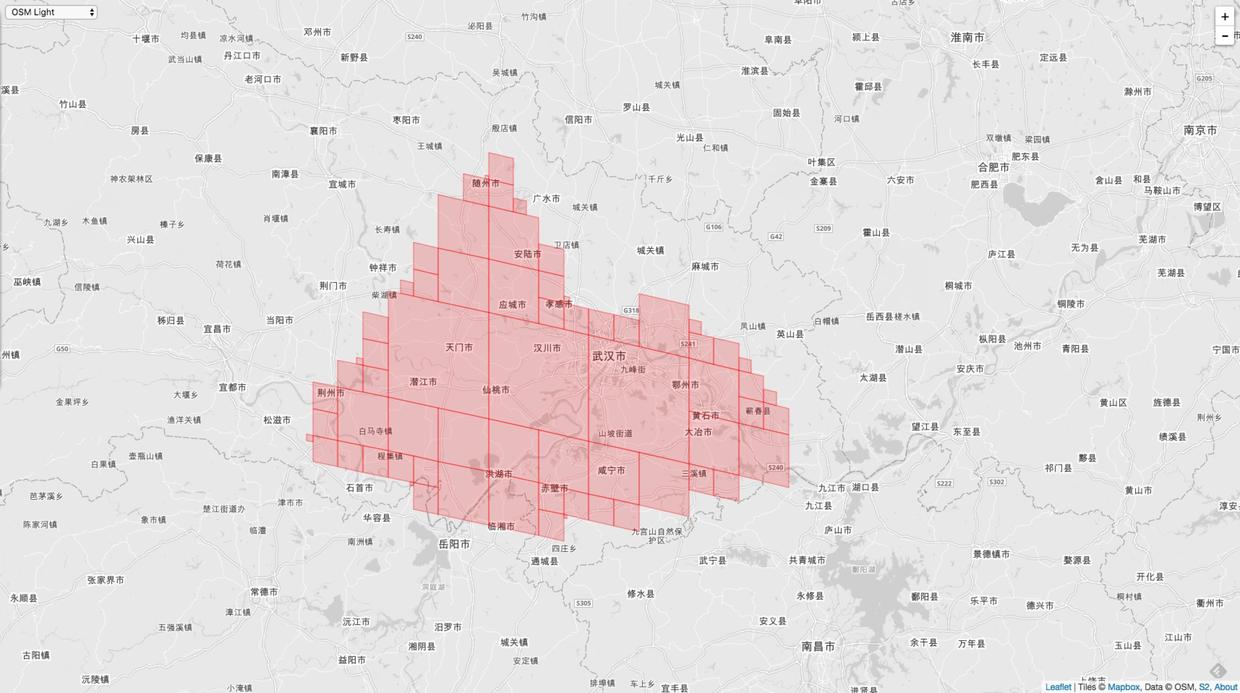
下图是 MaxCells = 1000 的情况：

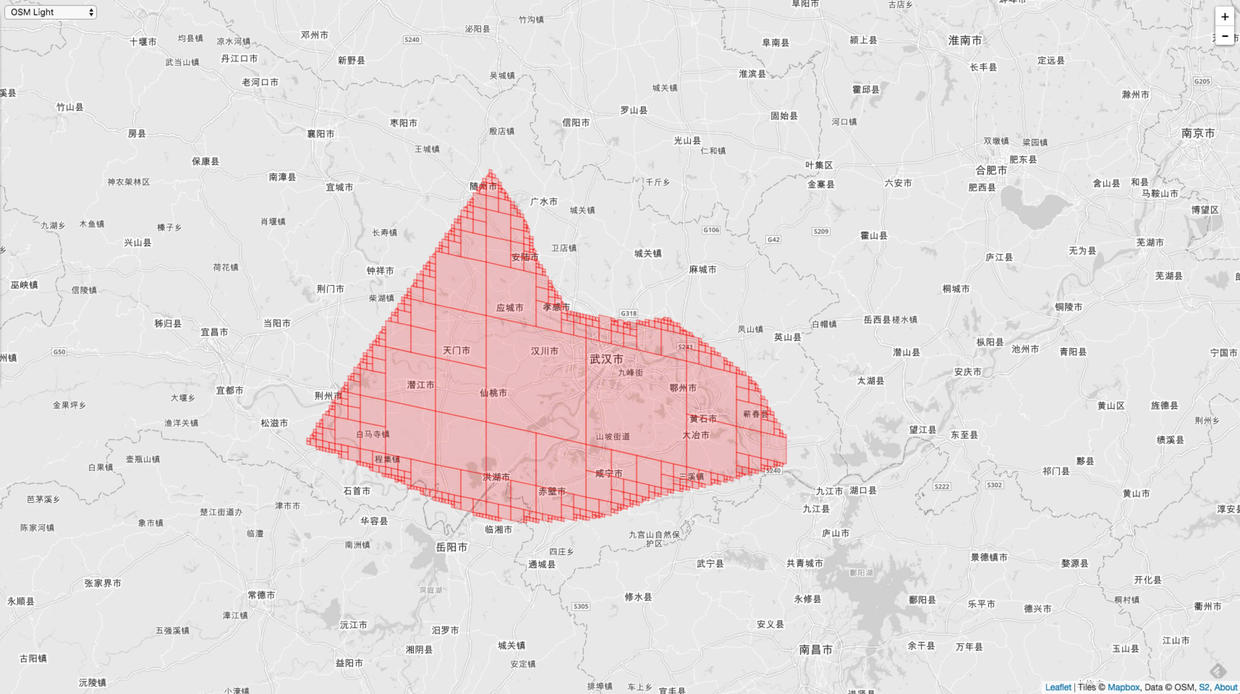
从这个例子也可以看出来 相同的 Level 范围，MaxCells 越精度，覆盖的精度越高。

9. S2 的应用

S2 主要能用在以下 8 个地方：

  1. 涉及到角度，间隔，纬度经度点，单位矢量等的表示，以及对这些类型的各种操作。
  2. 单位球体上的几何形状，如球冠（“圆盘”），纬度 - 经度矩形，折线和多边形。
  3. 支持点，折线和多边形的任意集合的强大的构造操作（例如联合）和布尔谓词（例如，包含）。
  4. 对点，折线和多边形的集合进行快速的内存索引。
  5. 针对测量距离和查找附近物体的算法。
  6. 用于捕捉和简化几何的稳健算法（该算法具有精度和拓扑保证）。
  7. 用于测试几何对象之间关系的有效且精确的数学谓词的集合。
  8. 支持空间索引，包括将区域近似为离散“S2单元”的集合。此功能可以轻松构建大型分布式空间索引。

参考文档：