空间搜索-Quad Tree
Quad Tree四叉树
四叉树 是一种非常简单的空间索引技术。在四叉树中,每个节点代表一个bbox,该bbox覆盖被索引空间的某些部分,而根节点则覆盖整个区域。每个节点要么是一个叶子节点-在这种情况下,它包含一个或多个索引点,并且没有子级;要么是一个内部节点,在这种情况下,它正好具有四个子级,每个象限一个子级,方法是将沿两个轴的一半-因此得名。
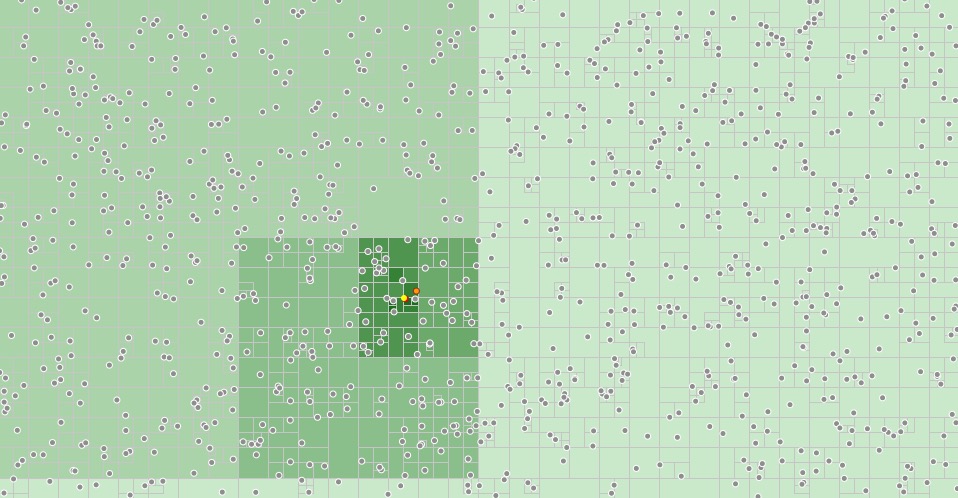
四叉树如何划分索引区域的表示。
将数据插入四叉树很简单:
从根开始,确定您的点占据哪个象限。递归到该节点并重复,直到找到叶节点。然后,将您的点添加到该节点的点列表中。如果列表超过了某些预定的最大元素数,请分割节点,然后将这些点移动到正确的子节点中。
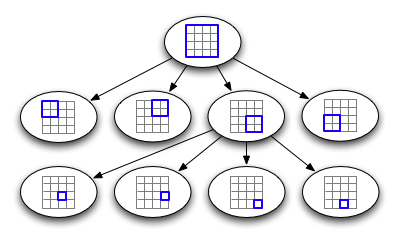
四叉树内部结构的表示形式。
要查询四叉树,请从根开始,检查每个子节点,然后检查其是否与要查询的区域相交。如果是这样,则递归到该子节点。每当遇到叶节点时,请检查每个条目以查看其是否与查询区域相交,如果存在,则将其返回。
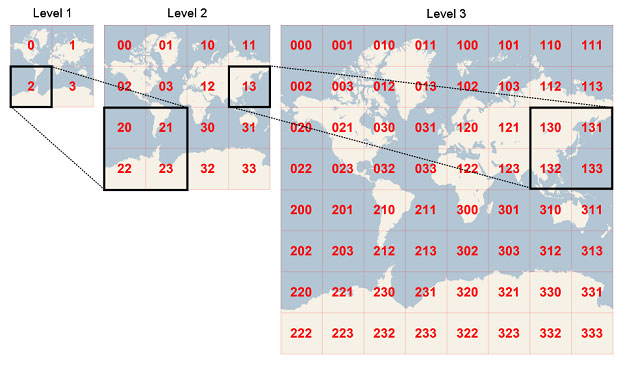
请注意,四叉树非常规则-实际上,它是Trie树,因为树节点的值不取决于要插入的数据。这样的结果是,我们可以以一种简单明了的方式对节点进行唯一编号:只需对每个象限以二进制编号(左上角为00,右上角为10,依此类推),而节点的数目就是串联从其根部开始,计算其每个祖先的象限数。使用此系统,示例图像中右下角的节点将被编号为1101。
如果我们为树定义了最大深度,那么我们可以在不参考树的情况下计算点的节点号-只需将节点的坐标标准化为适当的整数范围(例如,每个32位),然后将x和y坐标-每个位对在假设的四叉树中指定一个象限。
Lucene中的Cartesian Grid
Cartesian Grid方案,本质上就是QuadTree的一种变种,用来处理空间地理搜索。
显然,地球是一个3D的,需要先投影成一个平面。
Cartesian Grid使用的是Sinusoidal正弦投影方案,平面地图如下所示:
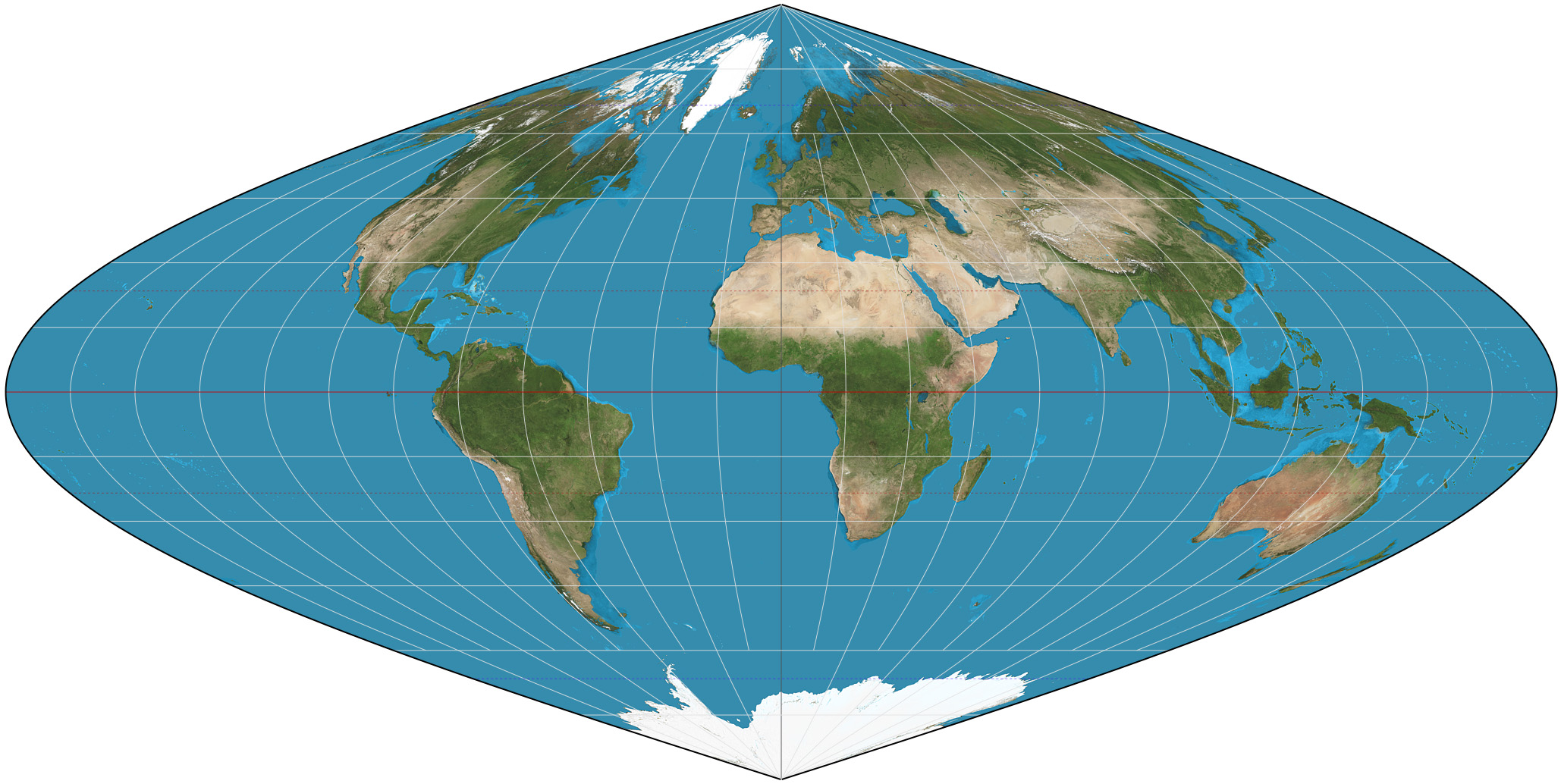
Cartesian Tier不断的往这个投影地图上覆盖,每个Tier的网格数是2的Tier id指数幂。
Tier 0有1个网格
Tier 1有2*2个网格;
Tier 2有 4*4个网格;
Tier 3有8*8个网格;
这样,任何一个地理坐标都可以放到这些不断细分的网格内。
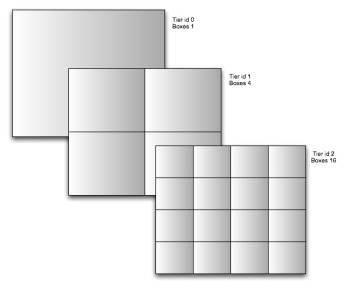
在Tier 15, 就有32768*32768个网格,这时网格的大小已经小于1英里了。
当不断往下细分,到第Tier 19(共20层)就能满足绝大部分的需求了。
那么,如果有一个需求,需要找E附近25英里内的数据,那么只要计算出距离E25英里的有哪些网格,然后去匹配搜索这些网格即可。如下图A,D,H,I,F,C,B可能就是一种答案。
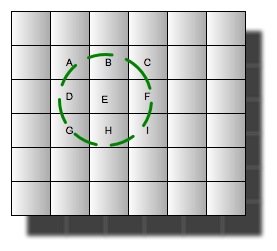
为了便于描述,需要为每个网格赋予一个唯一标识,这里称为Box ID。当然这个Box ID如果从Quadtree角度,是可以按固定的规则来一层一层的定义的,这个Box ID肯定也满足前缀树的特征。
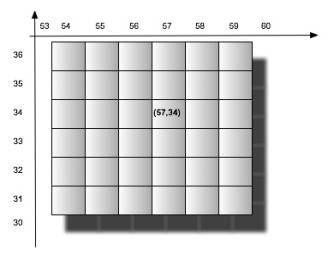
在lucene中,使用的Box ID计算方式有些不同,正常情况下一个2D数据就是一个(X,Y)来表示。lucene中是使用一个double类型来表示的,格式X.Y, 这主要是用来加快遍历速度,不再分2个坐标来分别遍历。
在一个256*256的网格内,一个box位于(57, 34), 那么它的Box ID=57.034。这里可以看到Y其实是被除以1000之后,添加到X后的。
为什么是1000呢,因为Y在256*256的情况下,离Y最近的10整数幂是1000,100显然不可以。
所以,在一个3000*3000的网格,(57,34)的Box ID应为57.0034, 此时Y应该除以10000, 1000已经不能Cover。
参考文档:
https://dzone.com/articles/algorithm-week-spatial
https://medium.com/@waleoyediran/spatial-indexing-with-quadtrees-b998ae49336
http://bl.ocks.org/patricksurry/6478178
http://www.nsshutdown.com/projects/lucene/whitepaper/locallucene_v2.html