空间搜索概述
空间搜索综述
空间搜索是针对多维空间数据进行的搜索,这听起来是一句废话。但是,这重点强调的是空间数据,而且数据是**多维(2D, 3D …)**的。同时, 空间搜索有别于传统的网页文本搜索(google, baidu等),传统搜索引擎针对的是海量的文本,分词之后,通过倒排等技术来进行快速的匹配。
空间搜索的数据则是点、线、多边形,多维空间等等几何体。如何能高效准确的搜索出想要的空间数据是空间搜索需要解决的。
在生活中无处不在
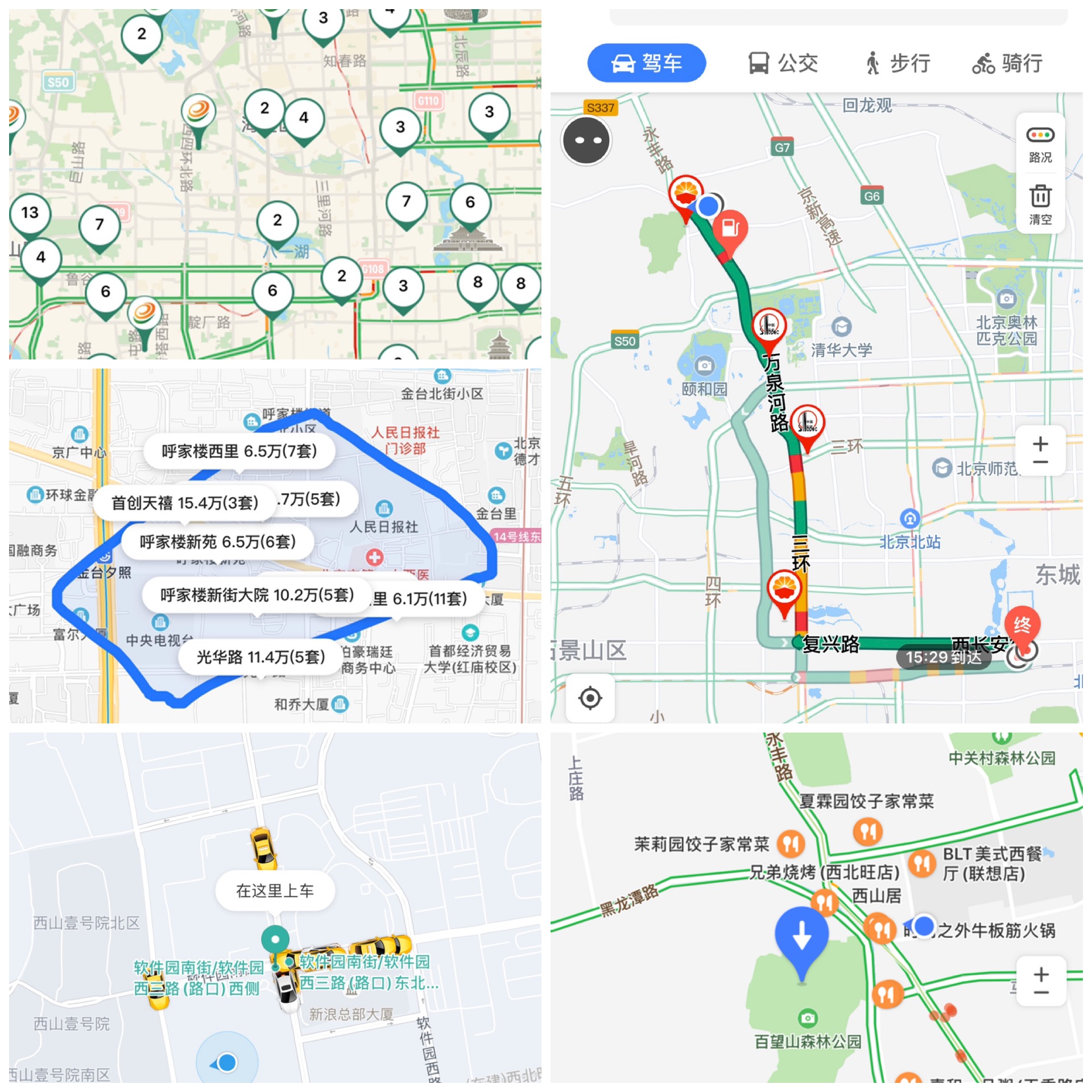
无形之中,空间搜索已经存在于我们生活中的方方面面。也许,出门你可能要打个车,看看附近有哪些司机师傅可以接单。自驾要搜索一下沿途的加油站,如果是电车你可能想找一下充电桩。抑或是你今天休息宅在家里,想找个餐厅,定个外卖。所有的这些都离不开空间搜索支持。
现在比较流行的RDBMS数据库 MySQL、PostgreSQL 都原生支持 B+ 树。这种数据结构能高效的查询。MongoDB、Redis等NoSQL数据库原生的支持了空间索引能力。业界对于空间搜索的需求是巨大的。
空间搜索解决2大核心问题
- 空间索引
- 空间查询
简单回顾一下,文本搜索似乎也是要解决这2个问题。也许文本搜索能给空间搜索带来一些启发。
文本索引是先切分为一个个的token词,然后针对每个token建立一个倒排链,也就是我们熟称的倒排索引。基本思想很简单,如下图所示:
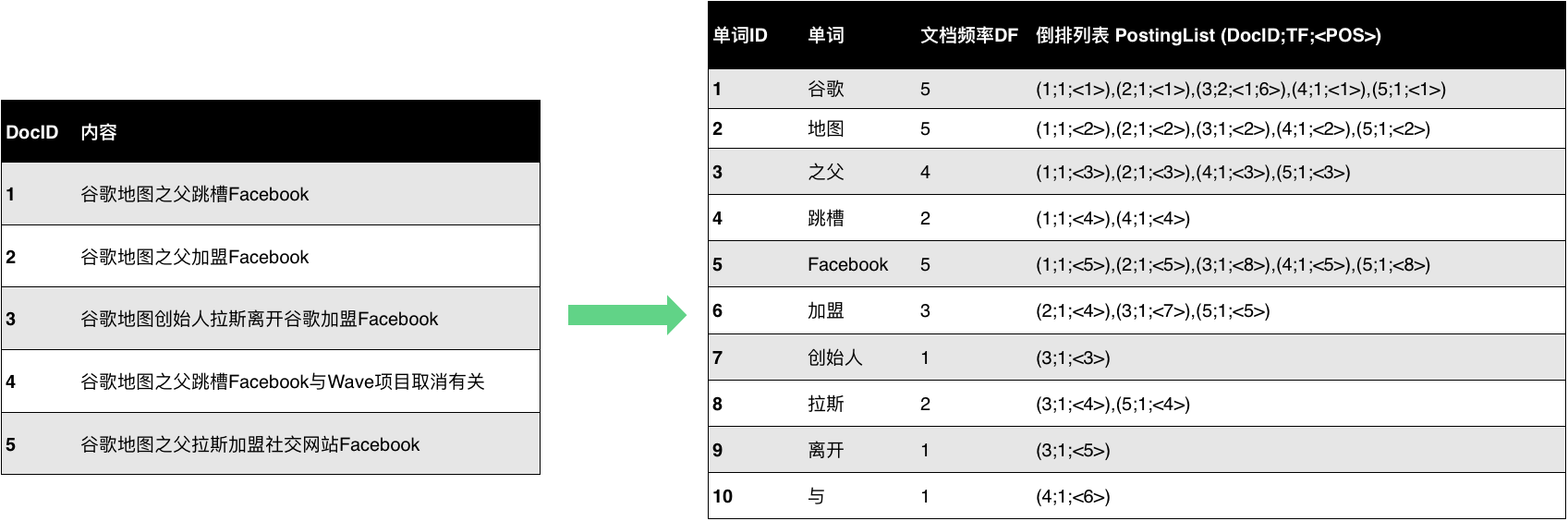
文本倒排索引建立之后,查询起来就特别快了。比如搜索”跳槽“,可以通过倒排链很快的得到1和4这两篇文档包含这个搜索词。这里需要注意的是搜索召回的时候只要包含这个搜索词,原则上就是我们想要的内容。
回过头来,我们来看一下,空间搜索的一个典型场景:
比如使用手机查找当前屏幕显示范围内的所有餐厅,或者离我2KM内(圆形)的餐厅,如下图所示。
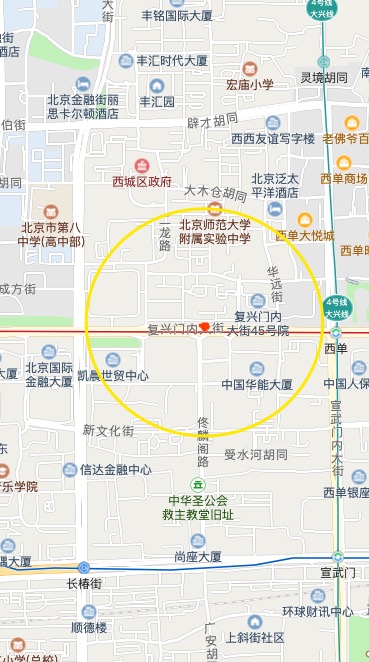
怎么来实现这个功能呢?
首先,想到的就是暴力法,扫描数据库内的所有餐厅,计算这个餐厅是不是在当前屏幕范围内,或者是不是离我当前位置2KM,然后把符合条件的餐厅过滤出来。
这个方案的确是可行的,但是显然是及其低效的。如果这个数据库餐厅的量级不断扩大,或者屏幕范围不断增大,这个计算耗时将是完全不可忍受的。另外还需要额外计算是否符合过滤条件(在不在范围内)。
既然如此低效,那我们可以如何改进呢?
低效的原因,在于全量数据扫描,如果有一种办法可以减小数据扫描量就可以了,在常见的关系数据库内,自然想到的就是加索引(index)。这就是通用的分治思想,诸如2分查找, 二叉搜索树, B+树等。这些都适用于1D数据的处理,针对地理位置点,这是一个经度和纬度构成的2D数据。
直观上来说,就是要把餐厅按照一定的规则归在不同的分块内,如果某个分块不符合过滤条件(比如附近2KM) , 那么整个分块内的所有餐厅也就没有必要再参与计算。通过分块,大大减少了计算量。
以上减少了扫描量,但是仍然是需要计算的,能不能做到像文本搜索一样,以常量O(1)的时间复杂度,高效的查询呢。这就牵涉出这样一个问题,如果能提前计算出附近2KM的分块是什么,那么直接使用文本搜索的倒排索引形式就可以常量复杂度解决问题。
为了能提前计算出附近2KM的分块,这对分块大小是有要求的,如果这个分块大小是100KMX100KM, 那有可能这个分块的内的数量仍旧是不可忍受的,还是会退化为O(n)的复杂度。但是如果分块太小,比如1mX1m,可能会导致满足条件的分块太多,从而导致整体性能的下降。 所以这是一个双刃剑。
所好的是,我们可以站在巨人的肩膀上,有很多前辈已经做了很多的研究和尝试,我们可以从中汲取营养,得到灵感。
空间索引基本步骤
综合以上提出的解决方案,实际上空间搜索的发展也是基本按照这样的思路来不断推进的。想做空间索引,至少以下几步都是不可缺少的。如下图所示:
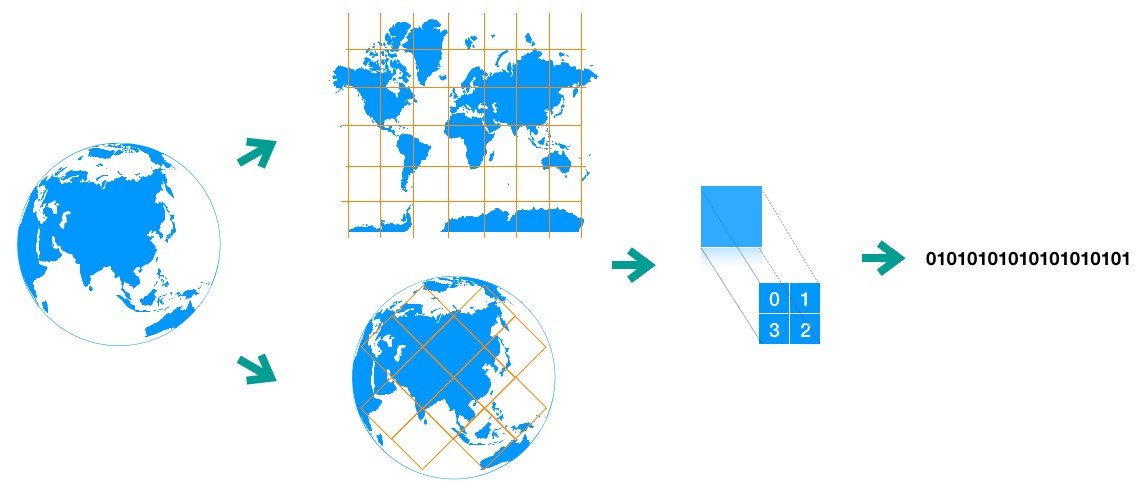
地球做为一个球体,她是3D的,虽然不是完全的纯球体。有人说他是一个椭圆形,由于自转的原因,赤道附近凸起,两极收敛的。也有人说,地球是一个梨形的,而且可能是个坏梨。
实际上,从海平面来说,地球就应该是像大家常见到的太空拍摄的图,蔚蓝色的,虽然实际上,可能并没有那么好看而已。大致可以认为地球是一个有点椭圆的圆形。
地球是一个3D是不争的事实,那第一步就是要考虑,我们是基于地球直接做分块呢,还是说基于更多认同的经纬度这一2D平面做分块呢。空间搜索这块,实际上不同的实现都有。
如果是基于经纬度2D,那么就牵涉到如何把3D地球映射为2D平面,这就是地球投影研究的范畴。
如果是直接基于3D球形做切分,那就要考虑如何在球面上做分块。其实这些事情远在计算机技术发明之前都有很多研究人员投入,那是地理信息科学研究的基础。可以参考基于地心投影,外接多边体方案的实现,这种方案通常称为测地线网格系统。
关于分块的大小,不同的业务场景其实是不一样的,有没有一种办法可以兼而有之, 有的。那就是分层,不同层有不同的块大小,这样在不同的距离上,选取适当的层来计算就可以了。当然,最好层之间是有包含关系最好,能够方便的在不同层之间转换,这也是全球网格系统研究的范畴,美滋滋。
分块不仅要考虑大小,还要考虑分块形状,块选取什么形状还是很有讲究的,当然我们自然想到的其实就是长方形、或者正方形。还有很多形状可以选择,但是并不是所有的图形都可以完全覆盖2D平面。
既然分块要有层次关系, 显然具有自相似性是最好的选择,这样无论你在任何一层来看,除了个数,大小不一样,形状应该都是一样的。那就要考虑,如何通过切分来划分为更精确的小块。简单来说,长方形就可以,可以不断的4等分,9等分等等。说的更有通用性,这是分形几何研究的范畴。
下面,我来分别的展开讲一下,空间搜索需要关注的各个部分。
地球是一个3D的
早期的空间搜索都是基于经纬度来处理的,毕竟这个广泛得到了人们的认同。
以常见的世界地图举例,其实我们默认接受了(经度、维度)这一笛卡尔坐标系,把地球通过投影,变成了一个2D的平面。无论我们使用的腾讯地图、百度地图,还是各种打车软件,其实都是基于这个平面地图来展开的。
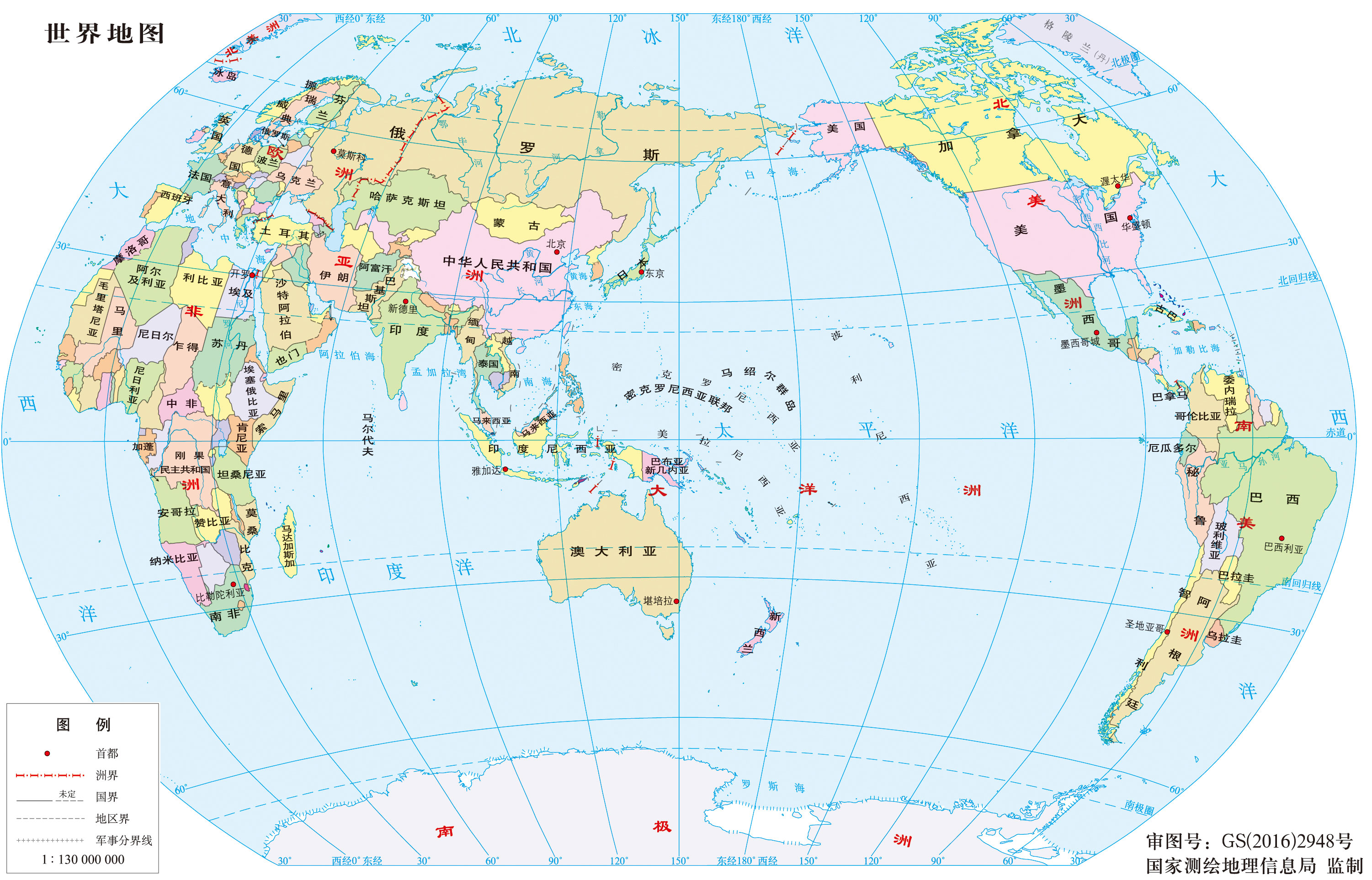
然而平面地图在处理空间搜索的时候是有一定的局限性的,这个局限性在于投影过程中导致的形状和大小的失真,由于失真的存在,可能导致数据分布不均,距离计算错误一系列问题。
地球是一个3D的,意味着在转为2D的平面地图之后,从经度,纬度上肯定是有变形的。这里暂不考虑地球本身就不是一个标准的球体,以及山川、湖泊、盆地的影响。直觉常会让人迷惑,比如下图。
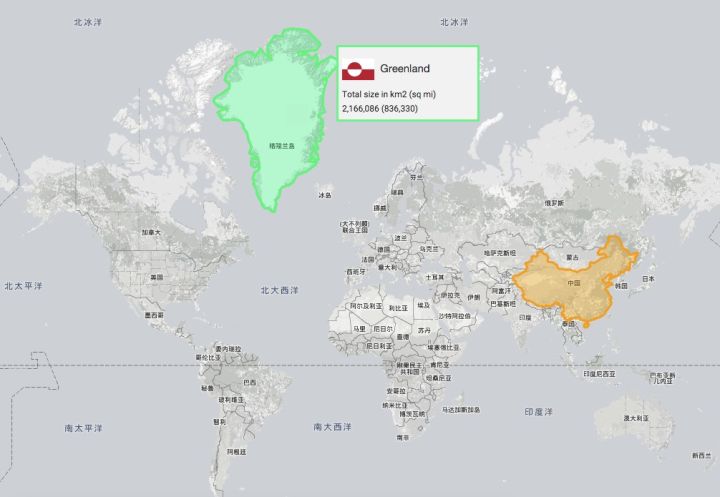
视觉上,格陵兰岛似乎比中国还要大,但是查询各种资料,发现它才216万平方公里大。中国大天朝可是有960万平方公里大。为什么会出现这种问题,这就是说地图在转换为2D过程中出现了变形,导致不同纬度在2D平面上的面积不一致,有误差。
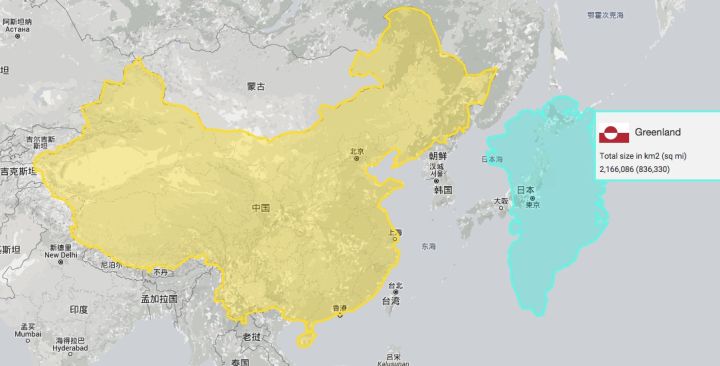
如果把格陵兰岛移动到和中国同纬度,那看起来就正常多了。比例也是对的。实际上,不同的转换方案可能导致的变形也是不一样的,这里的例子只是因为我们常用的墨卡托投影导致的一个副作用。
把地球从3D变为2D,这就是常说的降维, 在应用到地理信息系统时,有一个专有名词叫做地球投影。了解地球投影技术是理解空间搜索的一个基本。
以上,了解到了地球投影,以及它的劣势:失真。 那么下面我们来看一下,如何直接在地球3D上做分块, 这就引出了全球地理网格系统(DGGS)。DGGS研究范围,涵盖了如何分层,如何球面分块等等领域,下面来展开讲一下。
###全球地理网格系统(DGGS)
地理信息科学中的全球网格系统所要做的事情与空间搜索想做的事情不谋而合,或者说空间搜索的发展,直接借鉴了很多地理科学的研究成果。在地理信息科学(GIS)中,讨论如何划分网格(Cell)来表示地球, 从而可以让计算机来识别和高效查询已经有很多年的历史,成果丰硕。这使得空间搜索有了很好的理论基础。
单纯从DGGS发展来说,主要分为以下几种分类:
非分层网格系统
离散全局网格中最常见的一类是将网格中心点放置在经度/纬度子午线和平行线上,或者使用经度/纬度子午线和平行线形成矩形像元的边界的网格。从名字上也可以看出,这个是基于经纬度平面地图的网格系统,并且不是分层的结构。
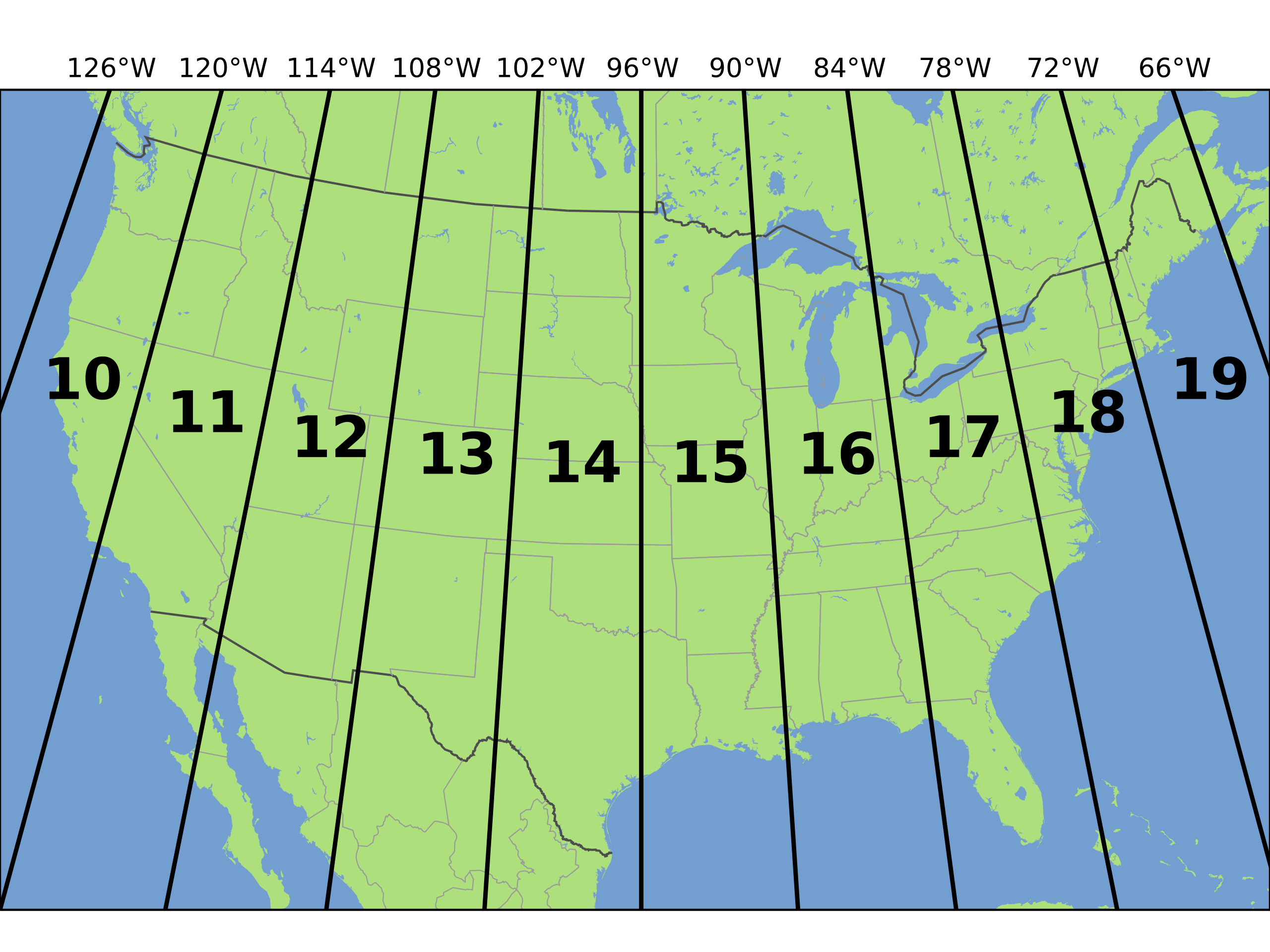
上图是针对美国UTM投影基础上,把美国按照6°的经度间隔进行分割的示意图。
分层网格系统:
相对于非分层网络而言。所谓分层,就是把地球逻辑上划分为N个层,每个层的比例尺是不一样的,用于来在不同的精度上来划分世界。
比如下图,显示了英国大不列颠岛的不同精度上的网格分布(150km比例尺、75km比例尺、37.5km比例尺)。
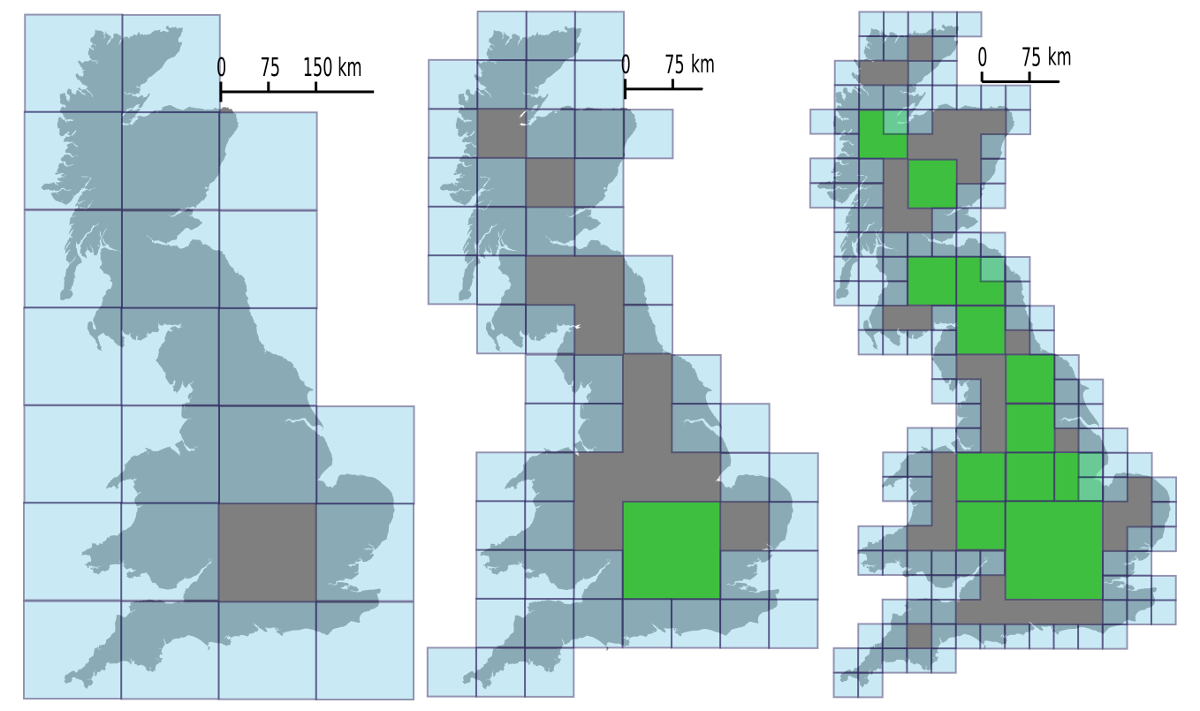
随着层次越高,比例越小,网格可以表示的区域也更加的精确。需要注意分层带来的好处,也就是图中绿色部分展示的效果,通过不同层次的结合,在更精细的比例上,同样是可以使用更粗的层次上来覆盖(Cover)的。这在空间索引,以及查询过程中,都能大大的优化存储量和查询性能。
测地线网格系统
普通网格系统,都是基于投影后的2D平面来切分网格的,且不论使用何种地球投影方案,这都会带来不同纬度的网格实际面积是不一致的,并且有可能面积相差很大。比如在赤道附近1°的距离,比靠近南北极的1°相差简直天差地别。
测地线网格系统,则是直接把地球按照测地线来作为一个3D球体来直接划分区域的。划分不受经纬度的影响,每个区域大小基本一致(地球不是纯球体)。在具体实现上,如何对地球表面的切分呢?
通常使用地球外接多面体,从地心投影的形式来划分:
基本上,一共有这5种正多面体可以来投影:正四面体、正六面体(正方体)、正八面体、正十二面体、正二十面体。

可以注意到的是,这些多面体都是正多面体(柏拉图体)。每个面的大小是一致的,完全符合网格切分的要求。显然面越多,面内部各自之间的区域失真就更低(面积小,地球起伏更低)。所以,常见的测地线网格系统多以正二十面体作为切分方案。如下图所示:
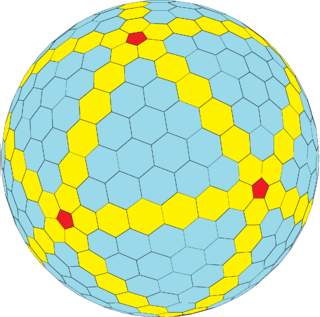
不是任何形状的网格都可以
无论是2D平面网格,还是直接在球体上做的切分,最终都是针对平面做的形状选择。测地线网格系统是先映射到了正多面体上。而每个正多面体的面,都可以近似作为平面来进行。
形状的选择,首先要考虑的是,什么图形可以完全覆盖平面。其实这和装修贴瓷砖是一个道理,选择什么样的瓷砖形状可以无缝密铺平面。实际上2015年华盛顿大学的数学系副教授卡西·曼、他的妻子珍妮弗及学生冯德劳发现了新的15种五边形可以密铺整个平面。这距离上一次发现类似效果的五边形已经有了30年。因此如何密铺,研究成果是很多的。
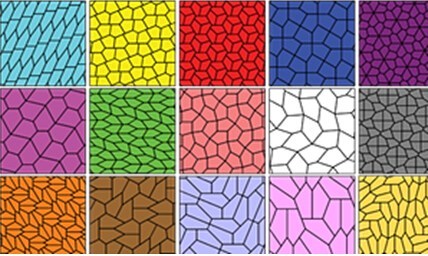
可以直接拿到的成果是:
任何三角形都可以密铺平面
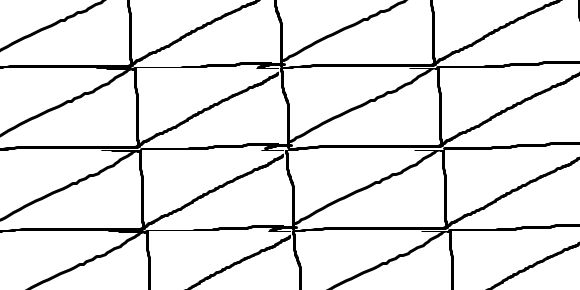
因为2个三角形何在一起就是一个平行四边形,平行四边形可以铺满。
任何凸四边形(正方形、矩形等)都可以密铺平面
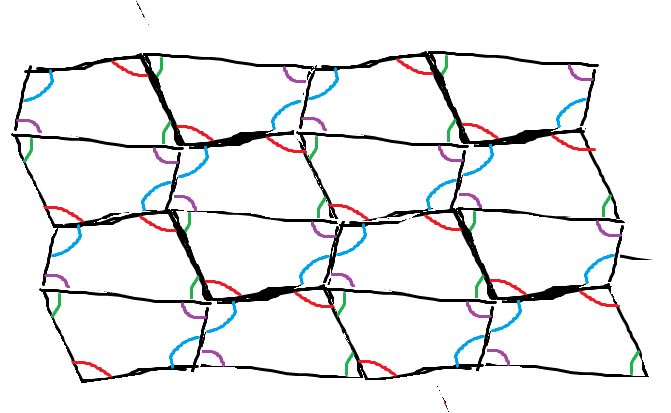
四边形内角和是360°,如果把四个四边形不同的角合在一起,那么就是360°。所以可以铺满。
正n边型中,只有正三角形,正方形,正六边形可以密铺平面。
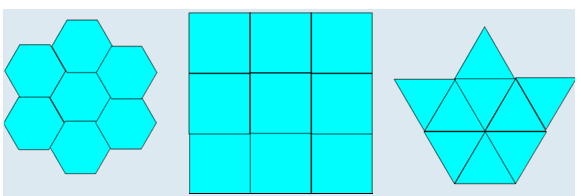
正n边型的内角和是
(n-2)*180°, 那么一个内角的大小就是n-2/n * 180°。 如果能铺满平面,内角的整数倍就应该是360°。得出n只能是3,4,6。
考虑到,要求网格必须有自相似性,以及数学计算复杂度。空间搜索的形状基本都采用矩形或正多边形。直观理解上,矩形和正方形是最容易接受的。
分层与编码
网格分层,要求网格形状最好是有自相似性以及精确包含。同时,倒排索引的要求,要求不同层之间的网格编码最好能有共同前缀,有共同前缀才能更高效的搜索。
提到了共同前缀,大家自然的可以想到Trie树,具备良好的前缀特性。其实任何树结构都具备前缀属性。树的层序遍历,可以方便的获取其子节点。双向树通过存储其父节点,可以查找他的父节点。
空间搜索也是这样的需求,那么如何给不同层的网格赋予ID,同时赋予其层次关系。
可以从第0层开始,每一层不断的往下N等分,给等分后的网格,按规则赋予编号(1,2,3,4…), 这样不断的迭代,直到想要的层次。
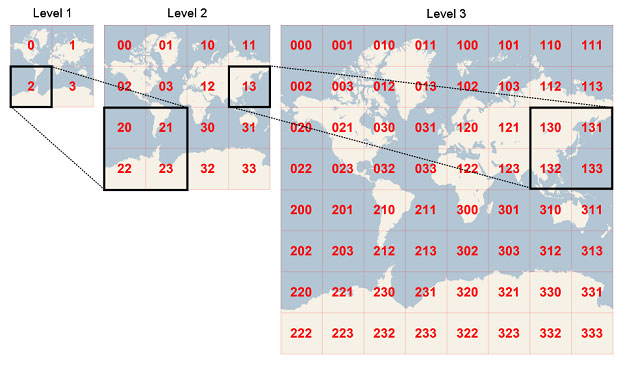
如上图所示,通过不断的4等分,一层一层的进行分割。其编码也具备前缀属性,当然这些编码也可以是ABCD, 规则可以自定义。其实上图表示的是四叉树结构。
当然也有,其他的N等分方案,比如3等分,7等分等, 依据选择不同的网格形状使用不同的切分方案。比如正六边形的分割方案。
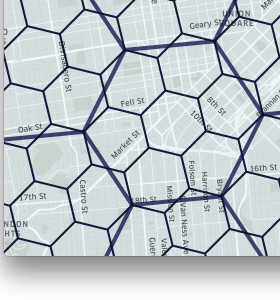
空间搜索网格方案
评价一个网格方案的好坏,至少要从以下角度来考虑:
- 网格形状是可以自切分的
- 更少的网格失真
- 网格系统是分层的
- 父子网格编码之间是可以高效运算的
- 网格之间距离计算高效
参考文档:
https://zhuanlan.zhihu.com/p/21110862
https://zh.wikipedia.org/wiki/%E6%B2%83%E7%BD%97%E8%AF%BA%E4%BC%8A%E5%9B%BE