空间搜索-分形几何
空间搜索-分形几何

分形(fractal)
分形(英语:fractal,源自拉丁语:frāctus,有“零碎”、“破裂”之意),又称碎形、残形,通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。 分形在数学中是一种抽象的物体,用于描述自然界中存在的事物。1975 年本华·曼德博首次提出“分形(fractal)”这个术语。
关于分形的具体定义,权威专家也仍有一些争论,即使作为”分形几何之父“,本华·曼德博也一直更新其定义。
“美丽、(研究起来)极其困难但又非常的有用,这就是分形”。1982年更新为:”分形是一种其豪斯多夫维数严格大于拓扑维数的集合“,后来称为”分形是由与整体在某些方面相似的部分构成的图形“ 。又过了一段时间,决定这样描述分形:“**…在研究和使用分形时,不需要迂腐的定义。用分形维数作为描述各种不同分型的通用术语**”。
通常认为, 理论分型是无限迭代、自相似的、具有分形维数的详细数学结构。
是不是看完以上的描述,还是不太了解什么是分形,那么我们来看几个现实中的例子。
| 花椰菜 | 蕨类植物 |
|---|---|
 |
 |
可以看出,每个花椰菜的凸起,单独拿出来其实都和花椰菜是一样的造型。蕨类植物的叶子,没个分支都和整体的形状一致。
本华·曼德博提出”关于英大不列颠岛的海岸线到底有多长?”这样的问题,他用分形几何给出的答案是无限长。
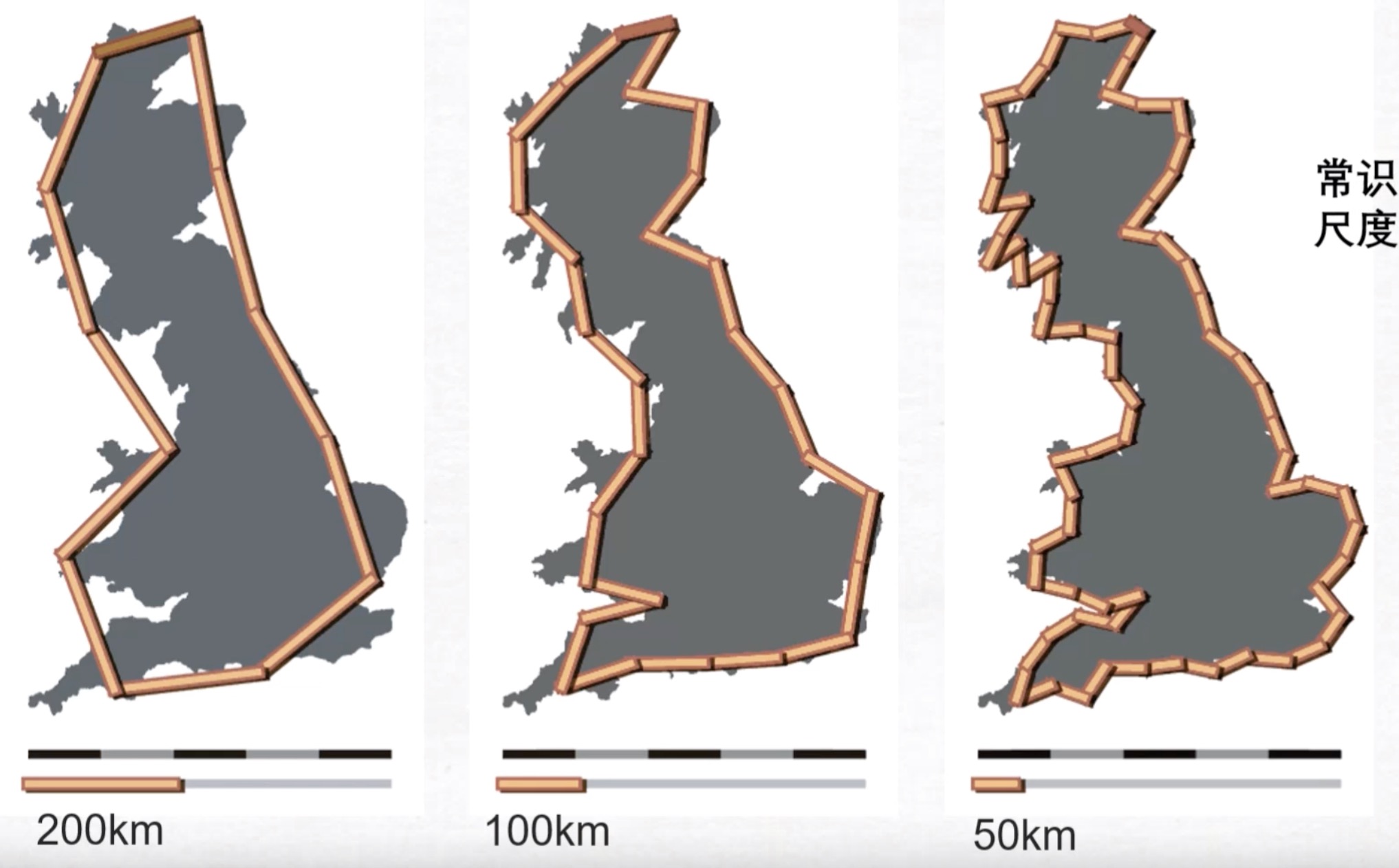
可以看出,在不同的比例尺下,去量海岸线的长度是不一样的。200KM比例尺海岸线约2300KM,而100KM比例尺则达到了2800KM,如果是50KM的比例尺,海岸长度达到了3500KM。试想一想,当比例尺越小,能够描绘的越精细,这个海岸线的长度也不断趋向于无限。
这个问题,回归到分形本身,其实就是针对直线这一图形,不断进行分形细分,直线分割越来越小。但是仍旧是一个直线(自相似)。
分形与其他几何图形相似但又有所不同。当你缩放一个图形时,你就能看出分形和其他几何图形的区别。将一个多边形的边长加倍,它的面积变为原来的四倍。新的边长与旧边长相比增加了 2 倍,而面积增加了 4 倍,即 2^2倍。平面内的多边形在二维空间中,指数 2 刚好是多边形所在的二维空间的维数。类似的,对于三维空间中的球,如果它的半径加倍,则它的体积变为原来的 8 倍,即2^3 倍,指数 3 依旧是球所在空间的维数。
如果将分形的一维长度加倍,如将康托三分集的初始线段长加倍,分型空间的内容2^n倍,此时n 不一定是个整数。幂指数n 称为分型的维数,它通常大于分型的拓扑维数。

要做出科赫雪花,将正三角形每边中央三分之一的线段以一对同长的线段取代,形成一个等腰的“凸角”。再对上一步骤所形成的每一边做同样的动作。每一次迭代,总长度增加三分之一。科赫雪花即是无限次迭代的结果,有无限长的周长,但其面积还是有限的。因此,科赫雪花和其他相似构造有时会被称为“怪兽曲线”。
下图是科赫雪花的动态展示: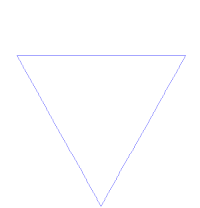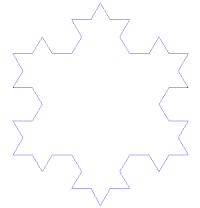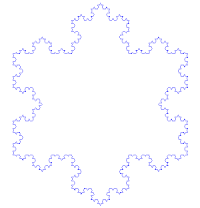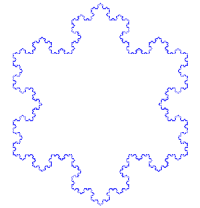
分形的“自我相似”的特征很容易通过类比来理解,就像用镜头或其他设备放大数字图像,从而发现以前不可见的、更精细的新结构。如果你放大一个分形的图像,则不会出现新的细节;图像没什么变化,相似的图案一遍又一遍的重复出现。对于有些分形几乎完全一样的图像会不断地重复。 自我相似的特征并非反直觉的。人们在生活中也能看到自我相似的现象,例如:两面平行的镜子间的无限重复、山上庙里老和尚的故事里的山…分形的不同之处在于重复的图案一定有详细的细节。
细节性的概念和分形的另一个特征——分形维数有关。分形维数不需要数学背景,也很容易理解:分形的分形维数大于它的拓扑维数,通过将分形尺度与普通的几何形状相比较,我们便能感受到他们的差别。举个例子,通常认为直线是是一维的,如果直线被分为三部分,每部分都是原来的 1/3 长,你会得到相等的三部分。相比之下,科赫雪花的拓扑维数是 1,和普通的直线一样,但它的分形维数大于 1,因为它有很多的细节。雪花曲线被分为原长的 1/3,得到的是 4 条原始雪花曲线重组组合的结果。这种与众不同的关系是分形维数的基础。
这也引出了第三个特征:分形在数学上是处处不可微的。具体的说,这意味着分形不能用传统的方法测量。测量非分型曲线,如波浪曲线的长度,只要放大到足够大,总能用直线拟合一小段曲线,然后就能用卷尺测量这段直线的长度,再将各段直线长度相加,就可以得出波浪的长度。这样做实质上是把曲线看作数学上的函数,在一小段范围内取一阶泰勒展开,近似为直线,然后求和总长度。但分型曲线是处处不可微的,如果尝试使用直线去拟合分形曲线,如科赫雪花曲线,缩放的过程永远不会停止,因为曲线图案的重复模式总会不断地出现,每次缩放,都需要使用更小的卷尺来贴合曲线。
分形一般有以下特质:
- 在任意小的尺度上都能有精细的结构;
- 太不规则,以至无论是其整体或局部都难以用传统欧氏几何的语言来描述;
- 具有(至少是近似的或统计的)自相似形式;
- 一般地,其“分形维数”(通常为豪斯多夫维数)会大于拓扑维数(希尔伯特曲线是相等的);
- 在多数情况下有着简单的递归定义。
因为分形在所有的大小尺度下都显得相似,所以通常被认为是无限复杂的。
一类分形的典型例子有: 康托尔集、龙形曲线,谢尔宾斯基三角形和地毯、门格海绵、、皮亚诺曲线等。
| 龙形曲线 | Gosper 曲线 | 谢尔宾斯基三角 | 谢尔宾斯基地毯 |
|---|---|---|---|
 |
 |
 |
 |
分形可以是确定性的,如上述所有的分形;也可以是随机的(即非确定性的)。
比如说,平面上布朗运动的轨迹的豪斯多夫维数等于2。实际上,布朗粒子的轨迹由大量无规则可循的折线组成,是一种处处连续但处处不可微的曲线,是一种无规分形曲线,它也具有自相似性,但这种自相似性具有统计的性质。
分形也可以依据其自相似来分类,有如下三种:
- 精确自相似:这是最强的一种自相似,分形在任一尺度下都显得一样。由迭代函数系统定义出的分形通常会展现出精确自相似来。
- 半自相似:这是一种较松的自相似,分形在不同尺度下会显得大略(但非精确)相同。半自相似分形包含有整个分形扭曲及退化形式的缩小尺寸。由递推关系式定义出的分形通常会是半自相似,但不会是精确自相似。
- 统计自相似:这是最弱的一种自相似,这种分形在不同尺度下都能保有固定的数值或统计测度。大多数对“分形”合理的定义自然会导致某一类型的统计自相似(分形维数本身即是个在不同尺度下都保持固定的数值测度)。随机分形是统计自相似,但非精确及半自相似的分形的一个例子。
现在有一些软件可以很好的画出精确自相似分形图形,甚至作为工艺品出售:

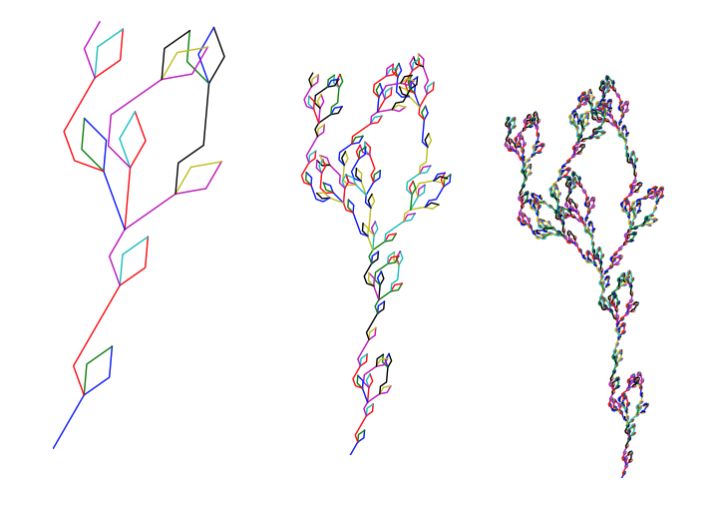
空间填充曲线
空间填充曲线目前来看其实就是分形的一种,它解决了这一难题:能否用一条无限长的线,穿过任意维度空间里面的所有点?
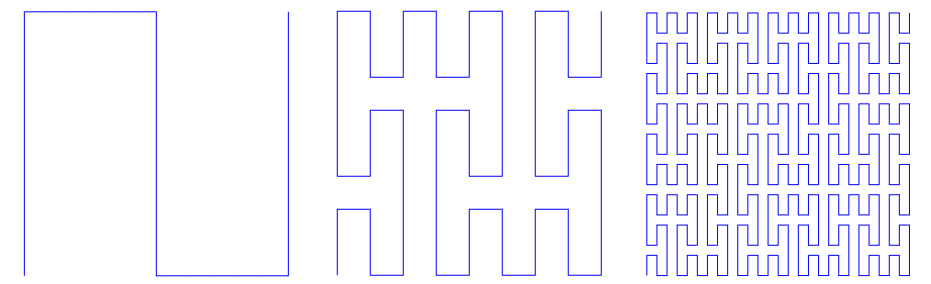
在1890年,Giuseppe Peano发现了一条连续曲线,现在称为 Peano 曲线,它可以穿过单位正方形上的每个点。他的目的是构建一个可以从单位区间到单位正方形的连续映射。 Peano 受到 Georg Cantor 早期违反直觉的研究结果的启发,即单位区间中无限数量的点与任何有限维度流型中无限数量的点,基数相同。 Peano 解决的问题实质就是,是否存在这样一个连续的映射,一条能填充满平面的曲线。上图就是他找到的一条曲线。
一般来说,一维的东西是不可能填满2维的方格的。但是Peano曲线恰恰给出了反例。
Peano曲线的构造方法如下:
取一个正方形并且把它分出九个相等的小正方形,然后从左下角的正方形开始至右上角的正方形结束,依次把小正方形的中心用线段连接起来;下一步把每个小正方形分成九个相等的正方形,然后上述方式把其中中心连接起来……将这种操作手续无限进行下去,最终得到的极限情况的曲线就被称作Peano曲线。
皮亚诺对区间[0,1]上的点和正方形上的点的映射作了详细的数学描述。实际上,正方形的这些点对于
一年后,即1891年,希尔伯特发明了另外一个曲线,叫希尔伯特曲线(Hilbert curve)。具体步骤如下。

上图就是1-6阶的希尔伯特曲线。
同样的原理,希尔伯特曲线也可以扩展到3D空间,如下图所示。

在数学分析中,空间填充曲线是一个参数化的注入函数,它将单位区间映射到单位正方形,立方体,更广义的,n维超立方体等中的连续曲线,随着参数的增加,它可以任意接近单位立方体中的给定点。填充曲线也是多种多样的。如下所示:

除了数学重要性之外,空间填充曲线也可用于降维,数学规划,稀疏多维数据库索引,电子学和生物学。空间填充曲线的现在被用在互联网地图中。
Hilbert Curve 希尔伯特曲线
希尔伯特曲线的定义
希尔伯特曲线一种能填充满一个平面正方形的分形曲线(空间填充曲线),由大卫·希尔伯特在1891年提出。由于它能填满平面,它的豪斯多夫维是2。取它填充的正方形的边长为1,第n步的希尔伯特曲线的长度是2^n - 2^(-n)。
希尔伯特曲线的构造方法

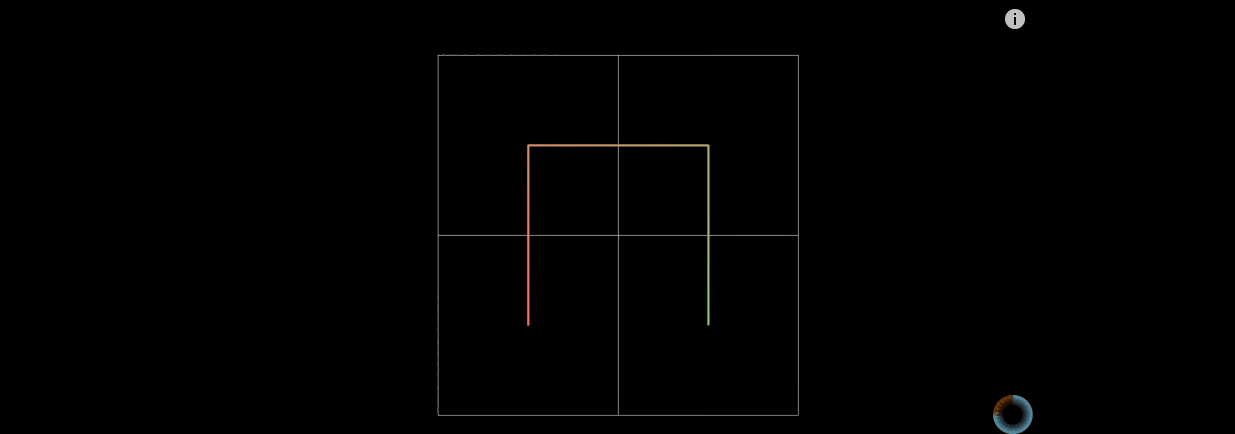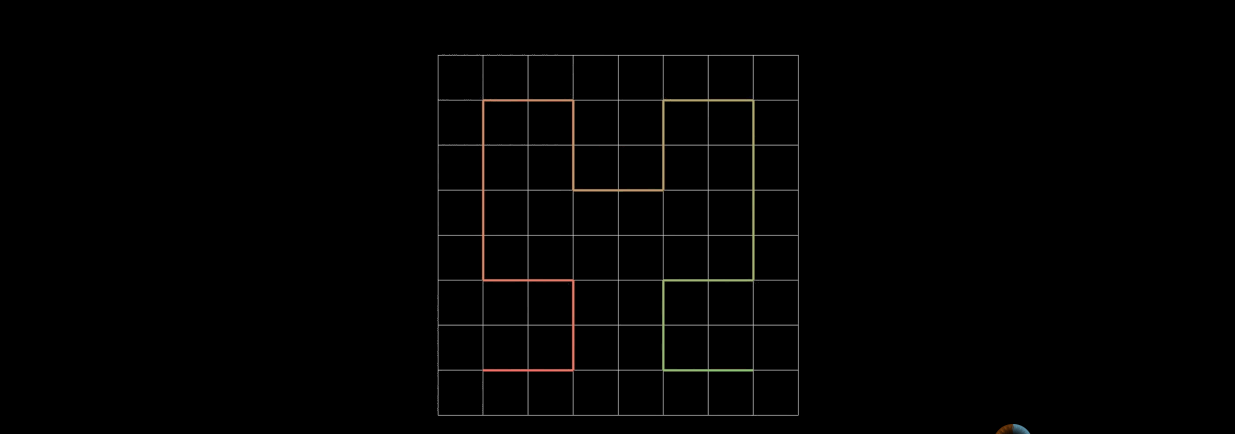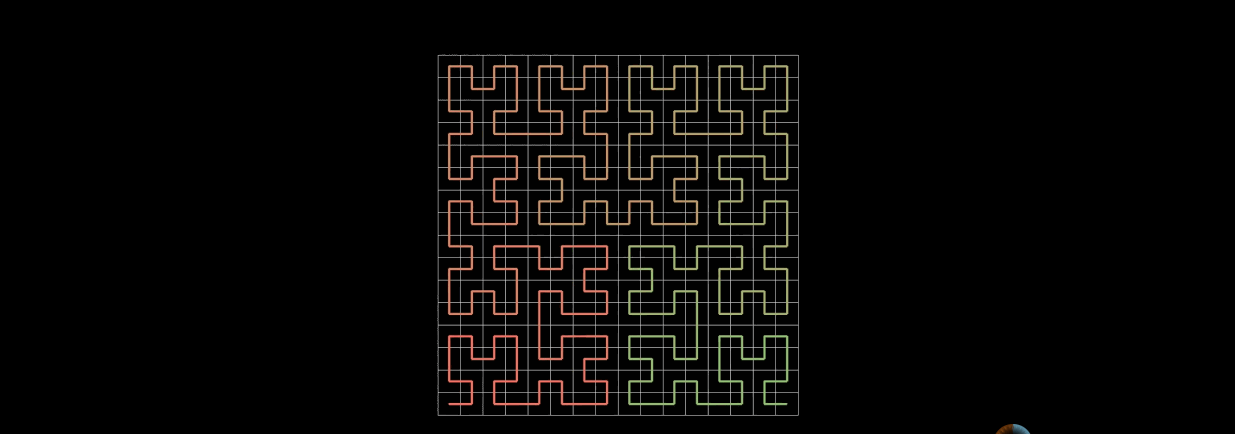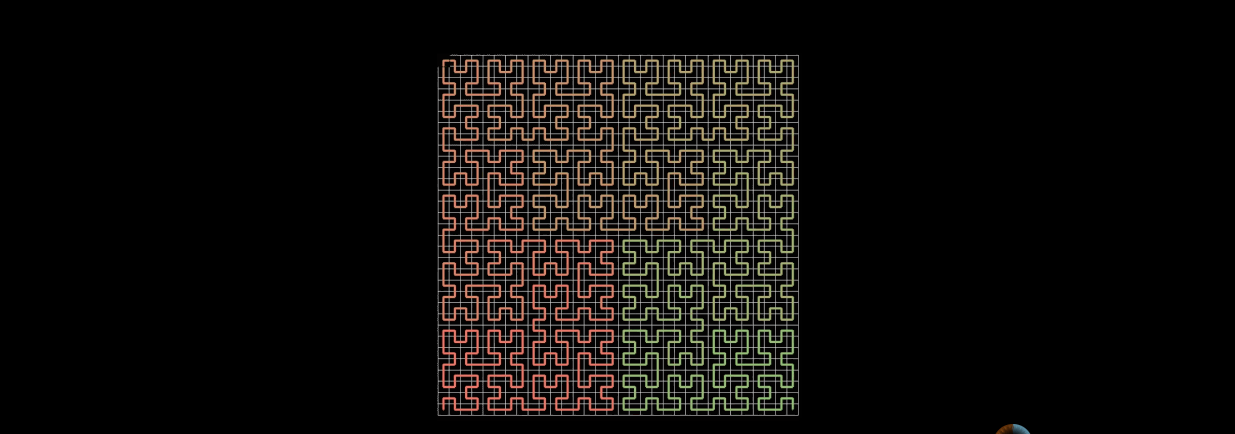
一阶的希尔伯特曲线,生成方法就是把正方形四等分(4个小正方形),从其中一个子正方形的中心开始(原则上从任何一个都可以),依次穿线,穿过其余3个正方形的中心。

二阶的希尔伯特曲线,生成方法就是把之前每个子正方形继续四等分,每4个小的正方形先生成一阶希尔伯特曲线。然后把4个一阶的希尔伯特曲线首尾相连。

三阶的希尔伯特曲线,生成方法就是与二阶类似,先生成二阶希尔伯特曲线。然后把4个二阶的希尔伯特曲线首尾相连。需要注意的是为了保证连续性,做了旋转操作。

n阶的希尔伯特曲线的生成方法也是递归的,先生成n-1阶的希尔伯特曲线,然后把4个n-1阶的希尔伯特曲线首尾相连。
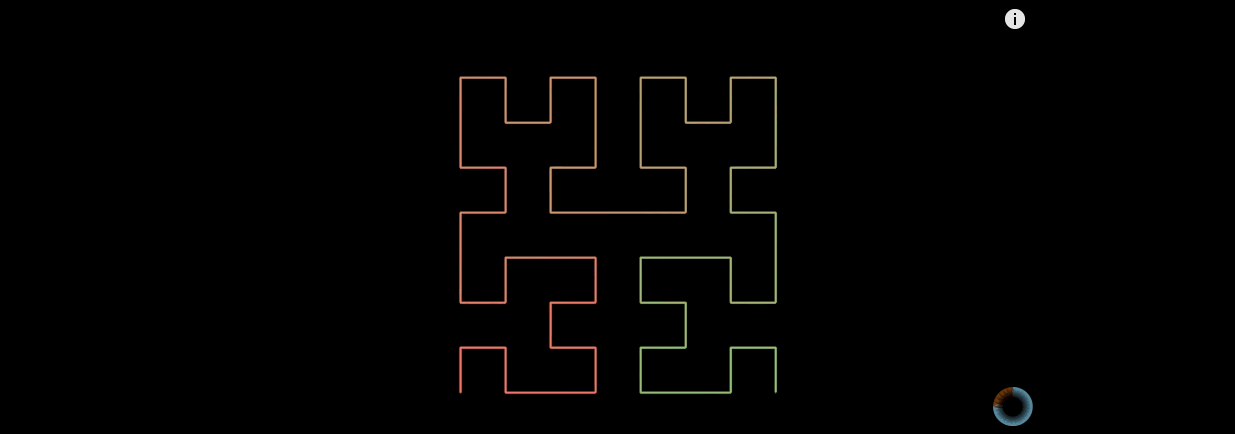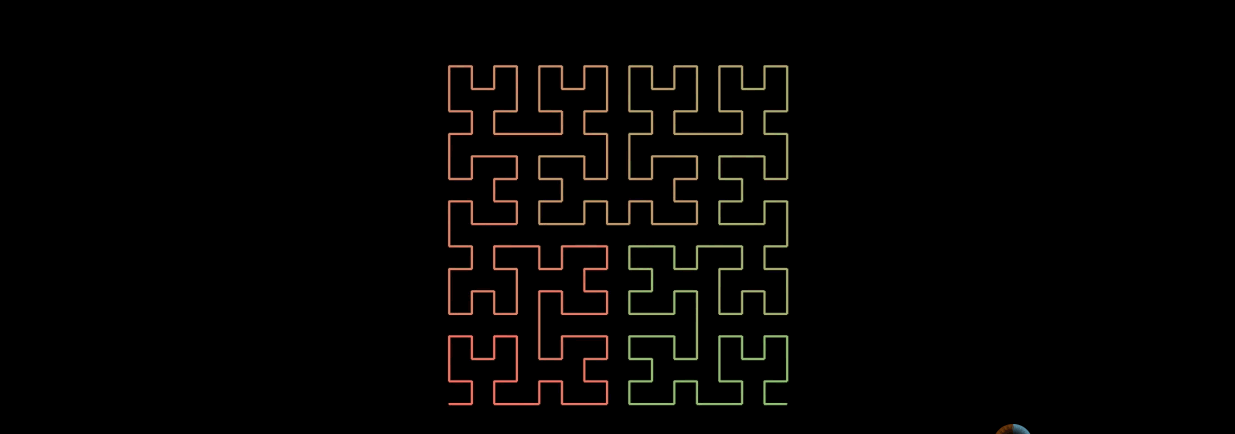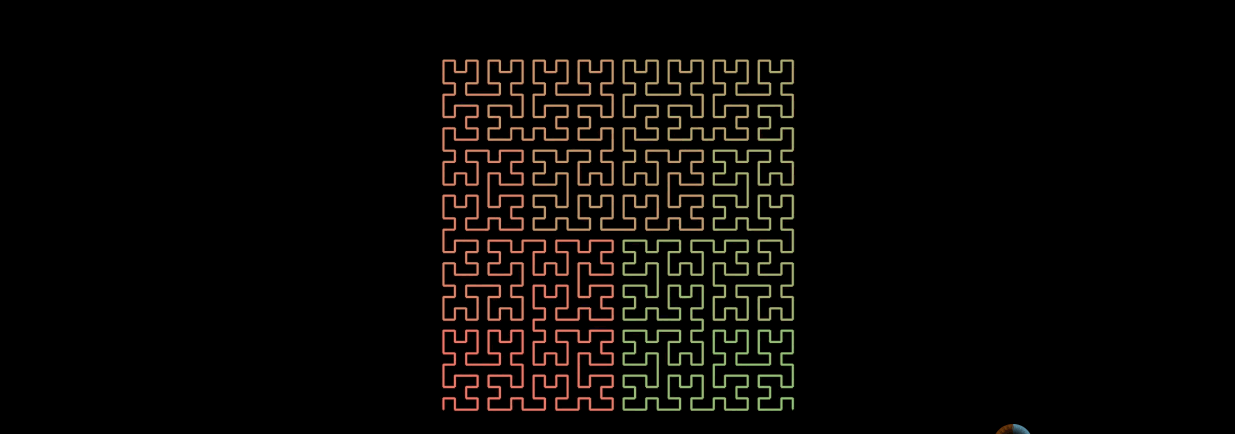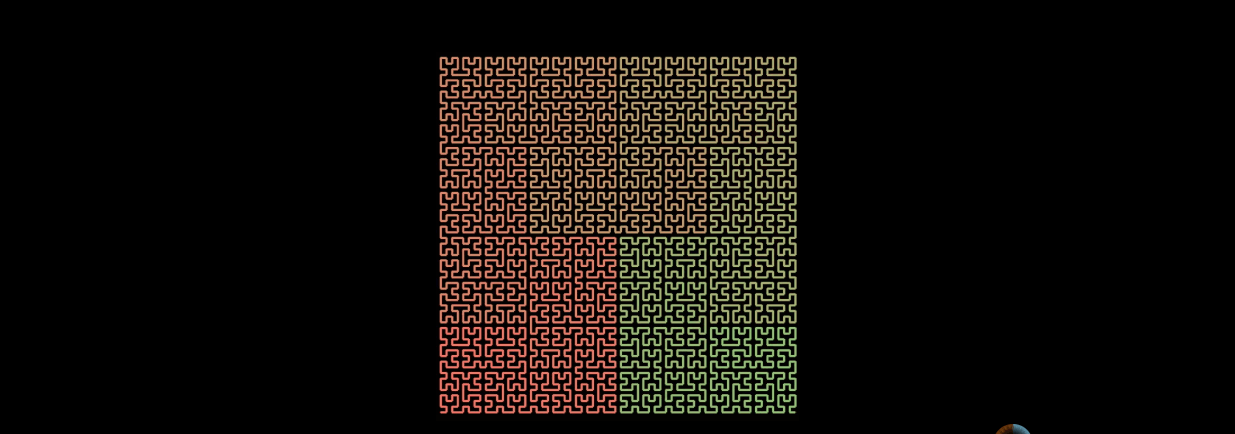
希尔伯特曲线特性
降维
作为空间填充曲线,希尔伯特曲线可以对多维空间有效的降维。希尔伯特曲线,本身就是对一条直线不断切分,生成的,从而可以填满2D区间。反过来说,这条曲线本身就是一维的。

上图就是希尔伯特曲线在填满一个平面以后,把平面上的点都展开成一维的线了。
当然,当n趋近于无穷大的时候,n阶希尔伯特曲线就可以近似填满整个平面了。这也是分形的特性,回到前面讲的“无限长的大不列颠岛的海岸线”。这里也是一样的,不但可以填满整个平面,从另外一个角度来说,这个线也是无限长的。当我们说这个长度是多少的时候,其实是有一个n来限制的。
稳定性
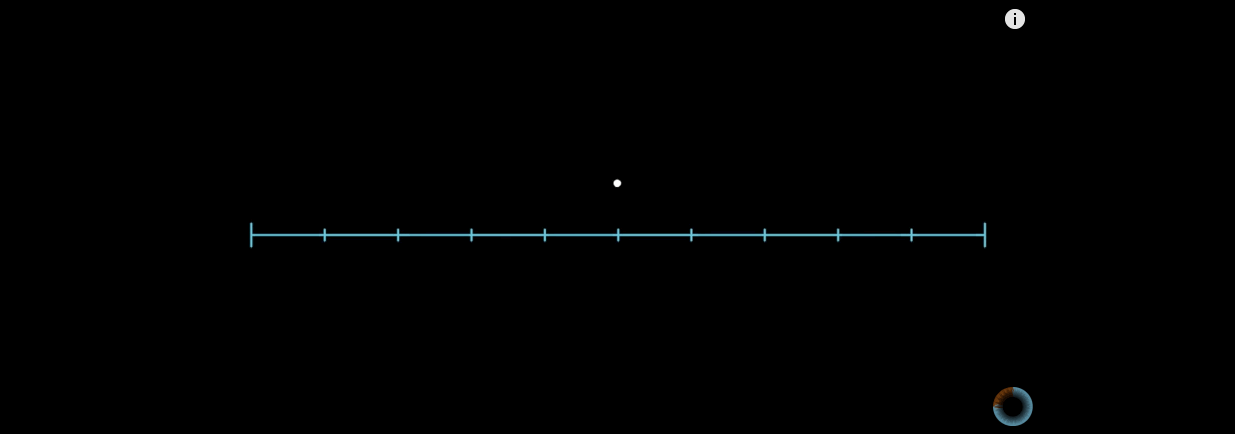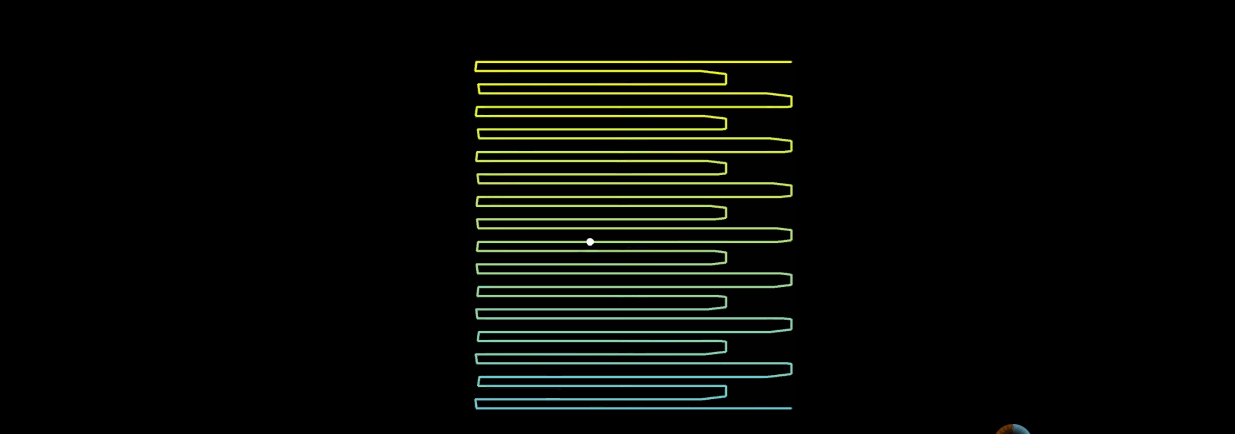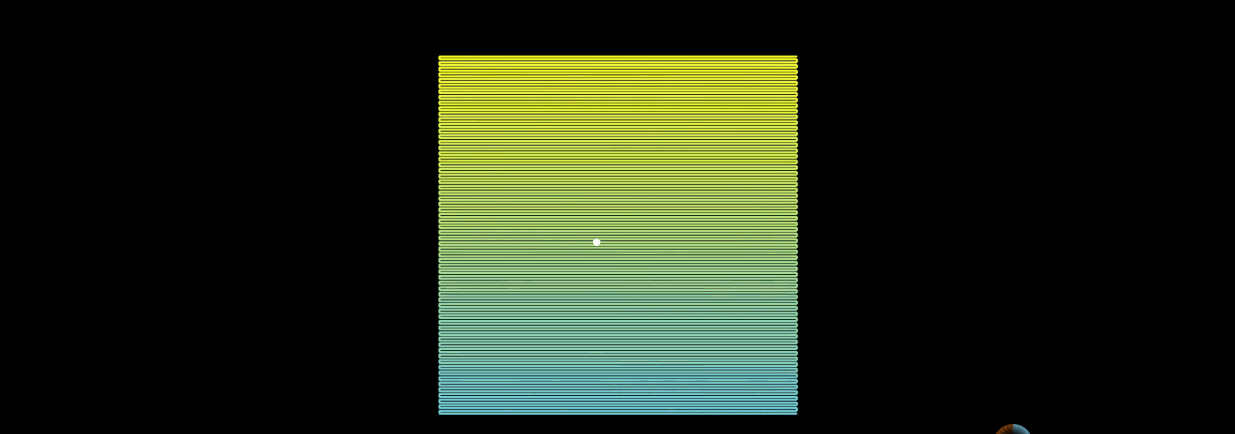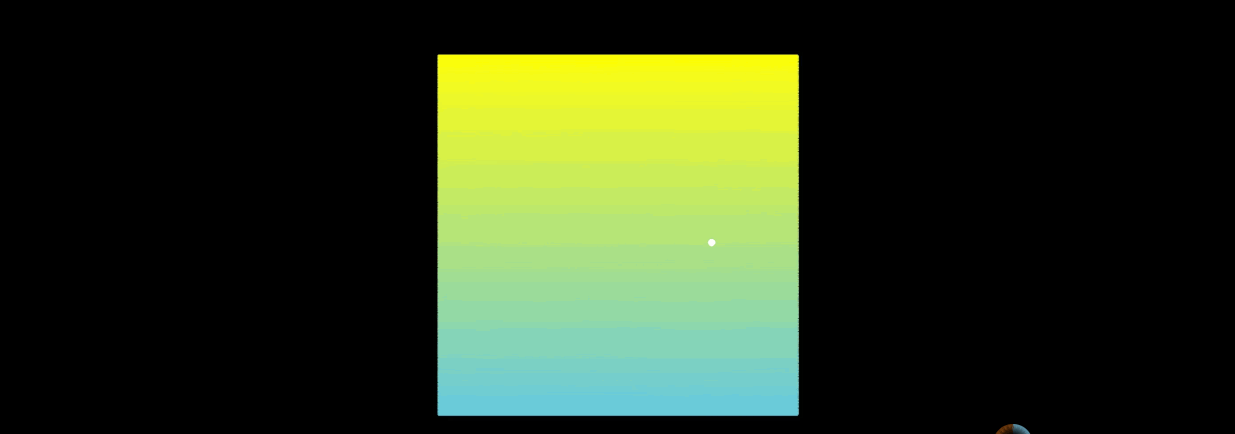
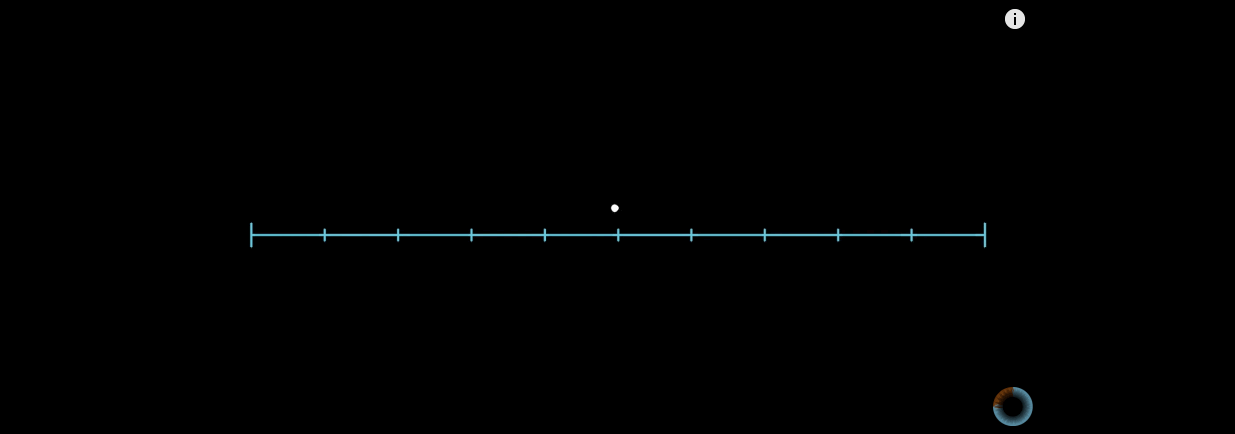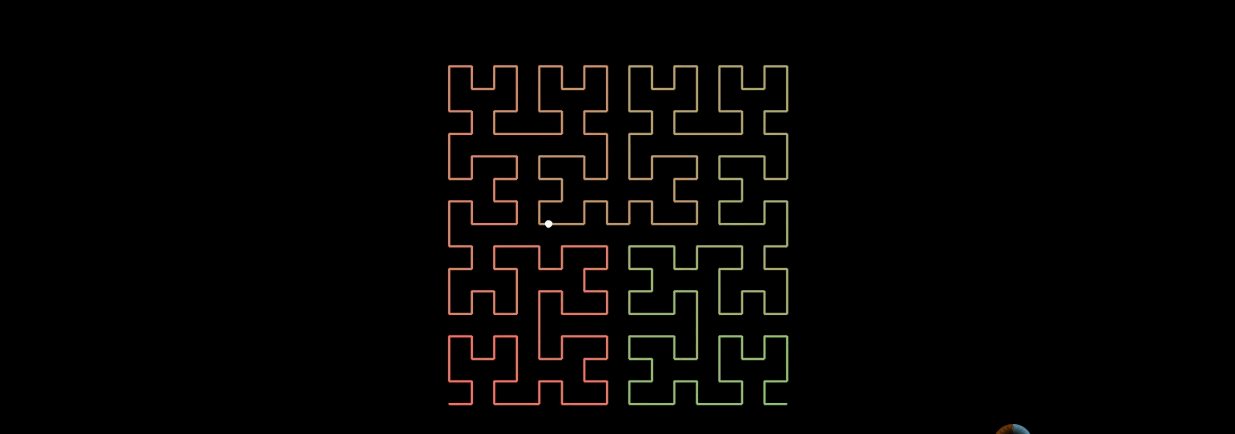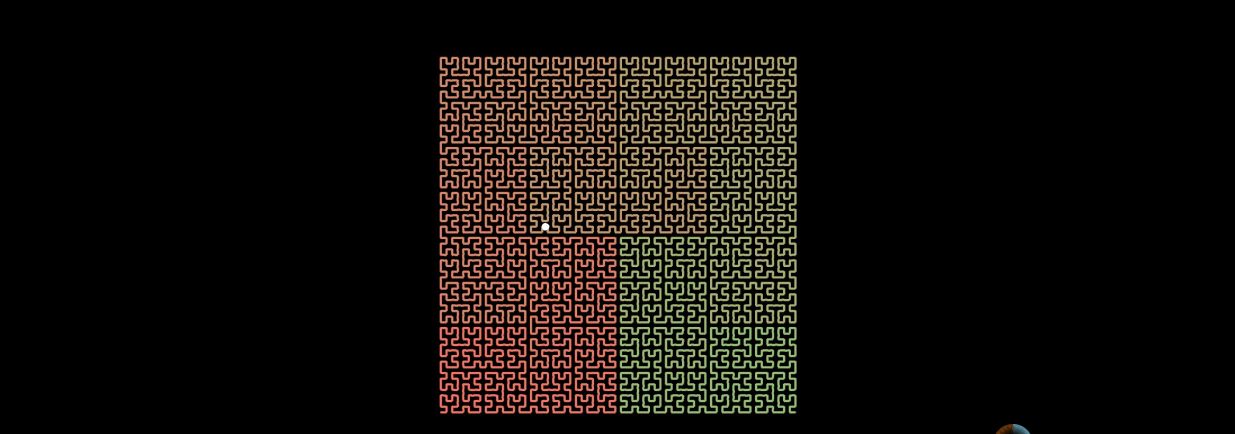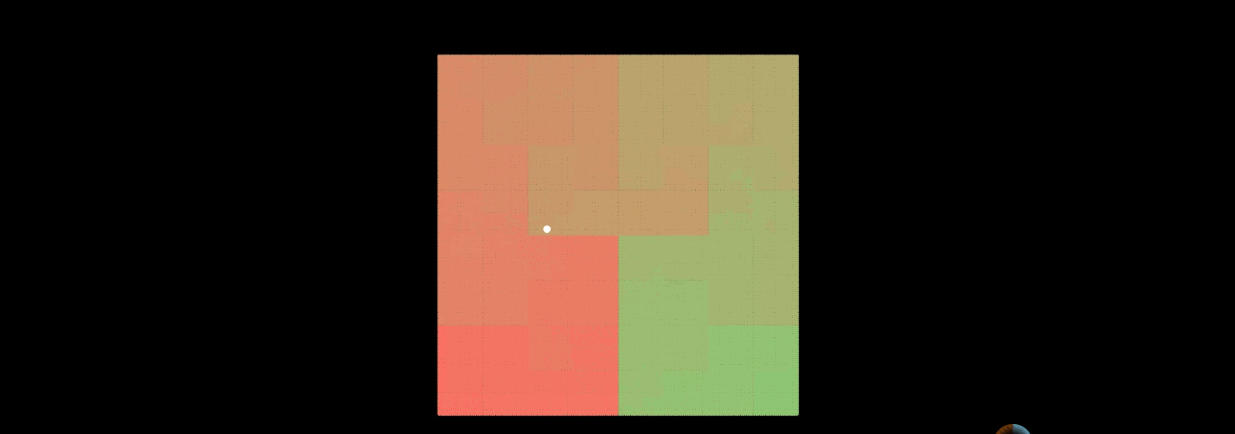
当n阶希尔伯特曲线,n趋于无穷大的时候,曲线上的点的位置基本上趋于稳定。举个例子:
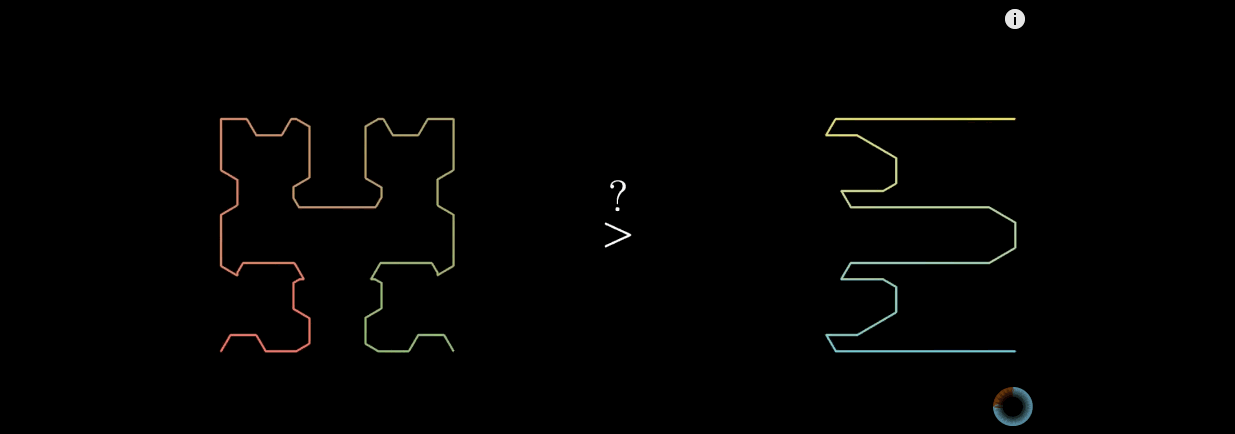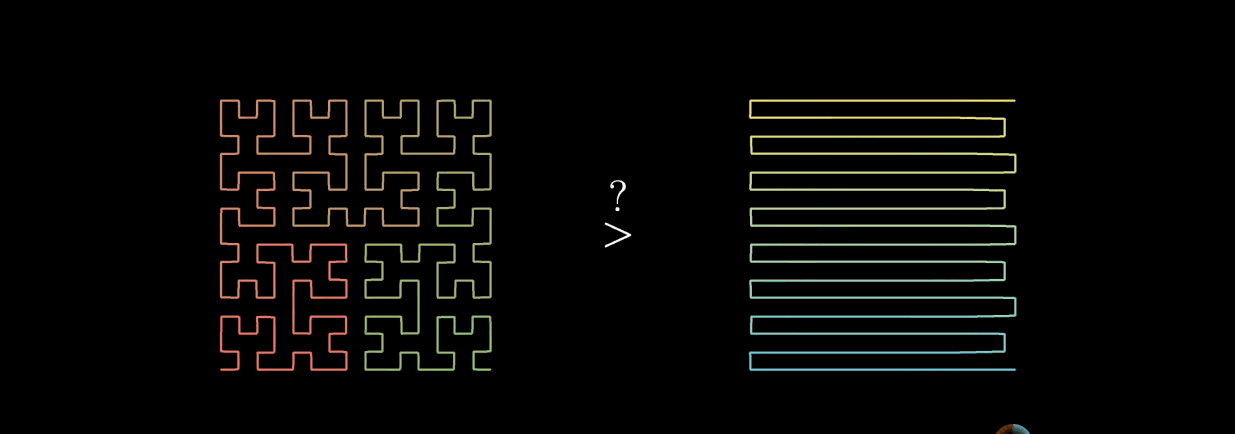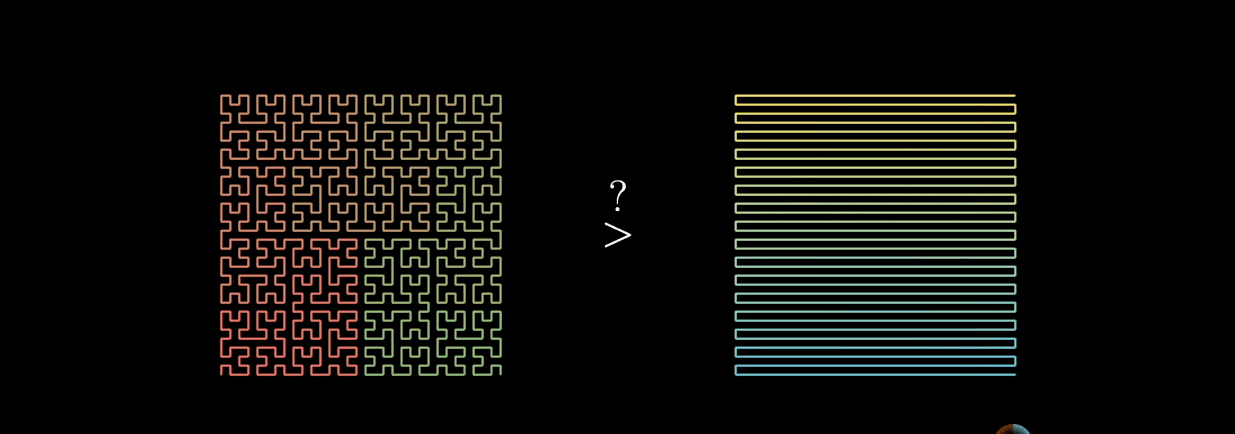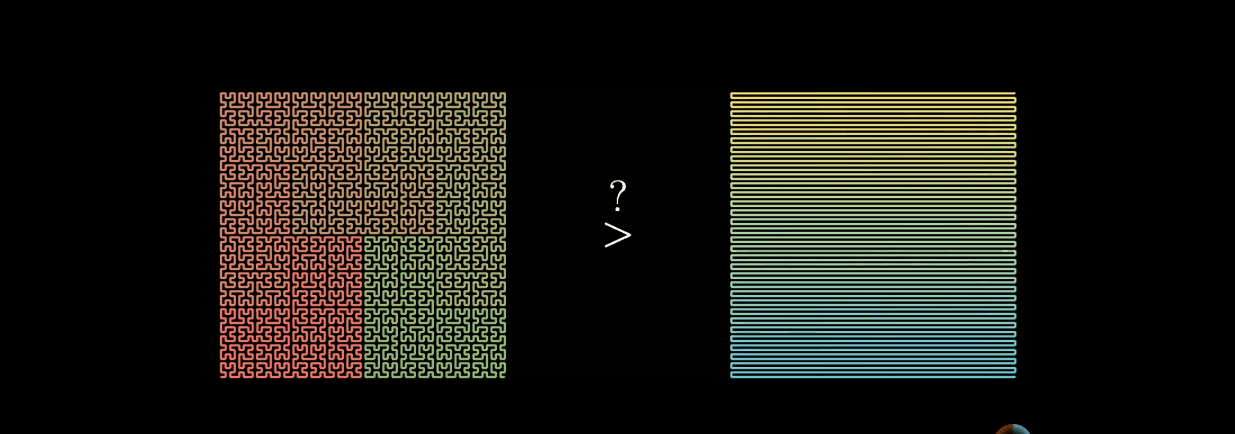
上图左边是希尔伯特曲线,右边是蛇形曲线。当n趋于无穷大的时候,两者理论上都可以填满平面。但是希尔伯特曲线更加优秀。
在蛇形曲线上给定一个点,当n趋于无穷大的过程中,这个点在蛇形曲线上的位置是时刻变化的。这就造成了点的相对位置始终不定。
 |
 |
再看看希尔伯特曲线,同样是一个点,在n趋于无穷大的情况下:
从上图可以看到,点的位置几乎没有怎么变化。所以希尔伯特曲线更加优秀。
连续性
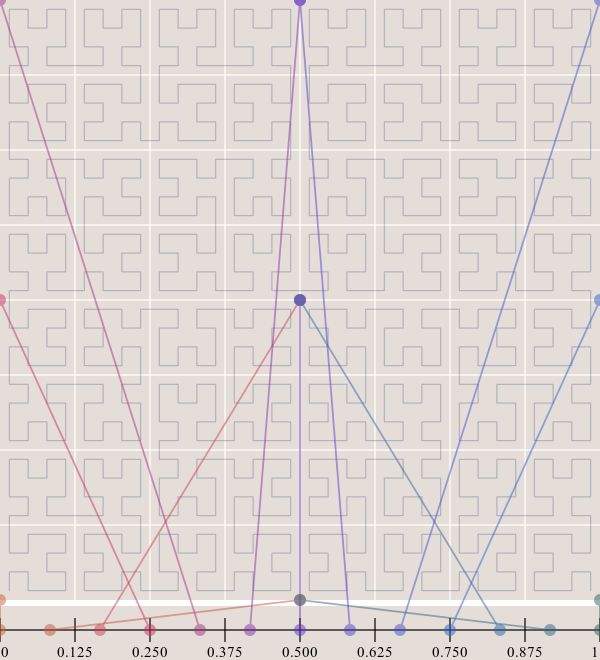 |
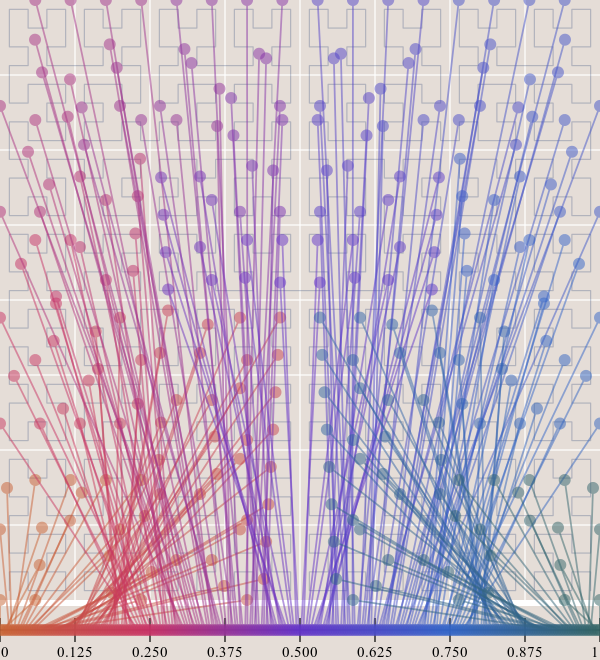 |
希尔伯特曲线是连续的,所以能保证一定可以填满空间。连续性是需要数学证明的。具体证明方法这里就不细说了。
参考文档:
http://blog.christianperone.com/2015/08/googles-s2-geometry-on-the-sphere-cells-and-hilbert-curve/?utm_source=tuicool
https://zhuanlan.zhihu.com/p/35358486
https://halfrost.com/go_spatial_search/
Space-filling curve
List of fractals by Hausdorff dimension
介绍希尔伯特曲线的Youtube视频
希尔伯特曲线在线演示
希尔伯特曲线论文
Mapping the Hilbert curve
伯努瓦.曼德勃罗:分形和粗糙的艺术
https://www.bilibili.com/video/av3602681/